ТЕОРЕМА ЗА КИНЕТИЧНИЯ МОМЕНТ НА МАТЕРИАЛНА СИСТЕМА

Фиг.1

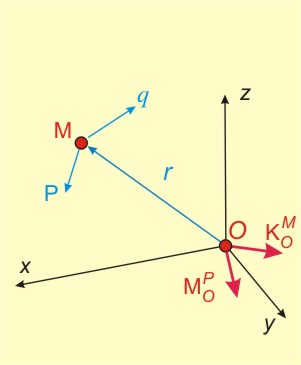
В предишна тема беше дефинирано понятието "кинетичен момент на материална точка" като векторно произведение от разстоянието до точката, за която търсим момента и количеството на движението (фиг.1) Ã:

.

Беше дефинирана и теорема за кинетичния момент на точка, изразяваща се с уравнението

,

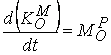където М_О^Р е момента на силата, действаща върху точката.

Фиг.2 ·

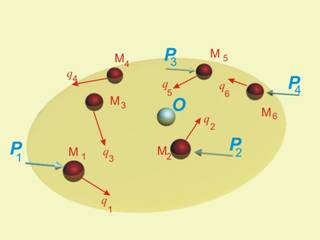
Когато разглеждаме механична система от точки, такова уравнение ще важи за всяка i^та точка (фиг.2):

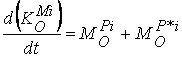Ã.

За материална система от n на брой точки ще се получи система от n на брой такива уравнения. От сумирането на левите и десните страни на тази система се получава ново равенство:

.

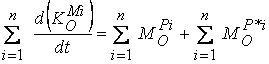Първият член на този израз може да бъде преработен така:

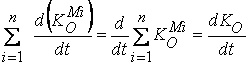, от където се вижда, че това е производната на главния вектор на кинетичните моменти К₀ по отношение на времето.

Вторият член е сума от моментите на външните сили - главен момент .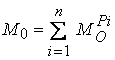

Фиг.3 ·

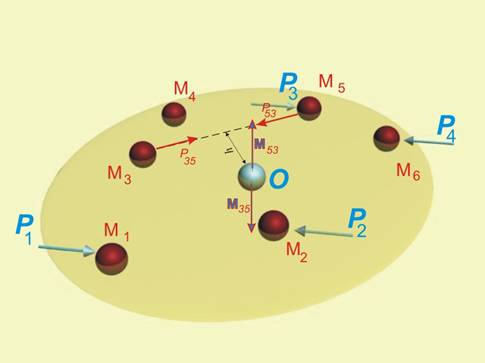
Третият член е сума от моментите на вътрешните сили. Тези сили се формират по пренципа на действието и противодействието между отделните точки. Нека да разгледаме една такава двойка вътрешни сили - силите на взаимодействие между т.М₃ и т.М₅ (фиг.3). Тези сили са равни,

Р₃₅ = Р₅₃ ,

но с противоположни посоки. Поради това техните моменти спрямо т.О също ще бъдат равни по големина:

Р₃₅ h = Р₅₃ h,

и с противоположни знаци:

М₃₅ = -М₅₃ , така че сумата им ще е нула:

М₃₅ + М₅₃ =0 .

Това важи за всяка двойка вътрешни сили, така че окончателно главният момент на вътрешните сили се получава нула:

.

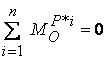Като се заместят получените изрази в основното уравнение 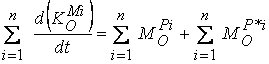, се получава окончателният вид на теоремата за кинетичния момент на механична система:

,

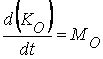или: производната по отношение на времето на кинетичния момент спрямо избрана точка е равна на главния момент на външните сили, приложени върху системата, спрямо същата тази точка.

Ако векторното уравнение 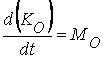се проектира върху осите на една координатна система, ще се получи теоремата в скаларната форма

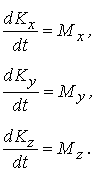
В частния случай, когато моментът на външните сили спрямо някоя от осите е нула, се получава законът за запазване на кинетичния момент. Например за оста х: 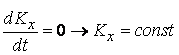, или: ако на външните сили спрямо някоя от осите е нула, кинетичният момент на системата спрямо същата точка е постоянна величина.

Фиг.4 ·

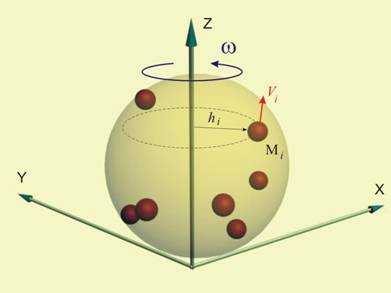
Теоремата за кинетичния момент най-често се прилага за тела, извършващи ротационно движение. Както вече знаете Ã, това движение се характеризира с ъглова скорост w и ъглово ускорение e. За прегледност (и за да избегнем интегралното смятане) при анализа на движението, тук тялото се представя като дискретна система от точки n на брой точки, отстоящи на разстояние h_i от оста на въртене z и движещи се по окръжност със скорост V_i = w h_i (т.М_i от фиг.4).

Количеството на движението на тази точка е:

q_i = m_iV_i = m_i w h_i ,

а кинетичният момент:

K_iz = q_i h_i = m_i w h_i h_i = m_i w h_i² .

Кинетичният момент на цялото тяло е сума от кинетичните моменти на отделните точки:

Това уравнение е известно още и като закон за запазване на количеството на движението. Ако този абстрактен начин на представяне на проблема не Ви допада или Ви затруднява, за да изкарате тройка на изпита е необходимо все-пак да илюстрирате действието на този закон със следния прост

r Пример №1 Количка и топче ·

В конкретните технически задачи теоремата се използва в нейния интегриран вид. Той се получава, като първо разделим променливите - всяка да е от различна страна на равенството:

® ,

и интегрираме между началния момент  и крайния момент ‚ на движението:

® .

Интегралът се нарича импулс на силата i ® I_i. Окончателният вид на уравнението става:

,

или:

Промяната на количеството на движението на системата е равно на сумата от импулсите на външните сили, действащи върху системата.

Понякога в техническите задачи е по-удобно да се работи с центъра на тежестта С на системата, като в него се концентрира цялата маса . По този начин количеството на движението става Q=M_cV_c. Като диференцираме двете страни на равенството:

® .

Това уравнение изразява теоремата за движение на масовия цинтър: масовият център на системата се движи като една точка, върху която са приложени всички външни сили, действащи върху системата, и с маса, равна на масата на цялата система.

За тройкаджиите (за отличниците - също): отново един прост илюстриращ

r Пример №2 Човек и лодка ·

ПРОДЪЛЖИ >>>