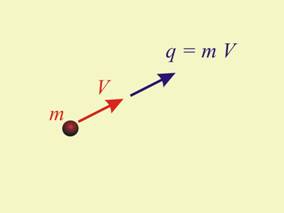
ТЕОРЕМА ЗА КОЛИЧЕСТВОТО НА ДВИЖЕНИЕТО НА МАТЕРИАЛНА ТОЧКА

Фиг.1

Количество на движението на материална точка, която има маса m и се движи със скорост v, се нарича векторната величина (масата по скоростта, фиг.1).

Направлението и посоката на количеството на движението съвпадат с тези на скоростта, а дименсията му е .

За извеждане на израз за определяне на q се изхожда от основното уравнение на динамиката Ã: Р=та. Ускорението се замества като първа производна на скоростта :

и масата прехвърляме под диференциала (позволено е, защото е скаларна величина и не зависи от времето):

.

Това уравнение е известно като теорема за количеството на движението на точка - производната на количеството на движението по отношение на времето е равна на силата, действаща върху точката.

В техническите задачи тази теорема по-често се използва в нейния интегриран вид. Той се получава, като първо разделим променливите - всяка да е от различна страна на равенството:

® ,

и интегрираме между началния момент  и крайния момент ‚ на движението:

® .

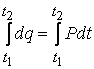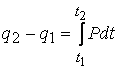Интегралът се нарича импулс I на силата. Окончателният вид на уравнението става:

,

или:

Промяната на количеството на движението за краен интервал от време е равно на импулса на силата, действаща върху точката.

Скоростта и силата са векторни величини, така че в техническите задачи решението често се провежда с помощта на проекциите на уравнението върху трите координатни оси - получава се система от три уравнения:

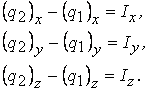
Сами ще трябва да се досетите, какво ще се получи, ако движението на точката е в една равнина или в едно направление. Но това касае колегите, които имат капацитет за усвояване на материала на ниво - оценка на изпита петица или шестица. Ако не сте от тях, необходимо е все-пак да демонстрирате действието на теоремата, например със следната задача: &

ПРОДЪЛЖИ >>>