ТЕОРЕМА ЗА КИНЕТИЧНИЯ МОМЕНТ НА МАТЕРИАЛНА ТОЧКА

Фиг.1

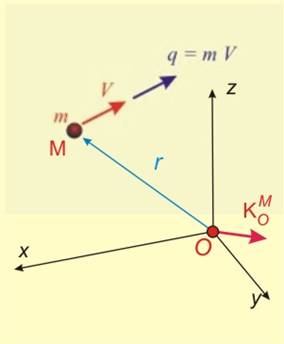
Кинетичен момент К_О^М на материална точка М, която има маса m и се движи със скорост v, спрямо произволна точка О, се нарича моментът на количеството на движението спрямо същата точка:

(фиг.1).

Големината, направлението и посоката на кинетичния момент се определят по правилата, дефинирани и за момент на сила спрямо точка Ã, а дименсията му е .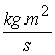

Подобно на момента на сила спрямо точка, и кинетичният момент е векторна величина и може да се проектира върху координатните оси, така, че да се получи кинетичен момент спрямо ос.

Израз за определяне на К_О^М може да се получи, като деферинцираме уравнението по отношение на времето:

® .

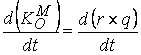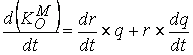В дясната част на равенството изразът се получи малко сложен, поради което се налагат обяснения:

- За първото събираемо

Производната на радиус-вектора е равна на скоростта ® . Количеството на движението е . Така първото събираемо става . Но векторите v и mv са колинеарни ( mv е същия вектор v, но с различна дължина, понеже е умножен с m). Поради това, векторното произведение .

- За второто събираемо .

Тук внимание заслужава членът . Той може да бъде преработен така:

.

Фиг.2

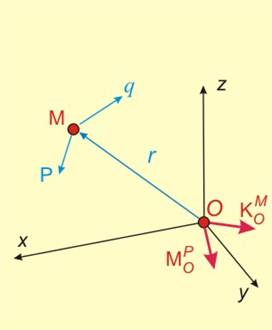
След като заместим тези резултати в уравнението за кинетичния момент, получаваме:

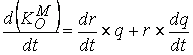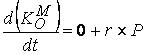® . Това, което се получи в дясно на равенството, по дефиниция представлява моментът на силата, действаща върху материалната точка, спрямо същата геометрична точка, за която търсим кинетичния момент: (фиг.2). Или окончателно

.

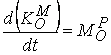Това уравнение е известно като теорема за кинетичния момент, която гласи:

Производната на кинетичния момент спрямо дадено точка е равна на момента на действащата сила спрямо същата точка.

В частния случай, когато моментът на силата спрямо избраната точка е нула, кинетичния момент е постоянна величина - спрямо тази точка важи теоремата за запазване на кинетичния момент:

.

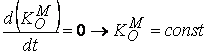Същото важи за моментите спрямо дадена ос.

Действието на теоремата ще демонстрирам с пример: &

ПРОДЪЛЖИ >>>