Момент на сила спрямо точка и ос . Двоица сили.

Когато разглеждахме условията за равновесие на точка, анализирахме действащите сили по правилото "има равнодействаща > има неравномерно движение > няма равновесие" (ако сте пропуснал този материал, по-добре се запознайте с него сега). Ако равнодействащата е нула, точката остава в покой или в равномерно праволинейно движение (равновесие). Когато разглежданият обект не е материална точка, а съвкупност от точки или материално тяло, това правило не е достатъчно.

Фиг.1 (щракнете тук за анимация)

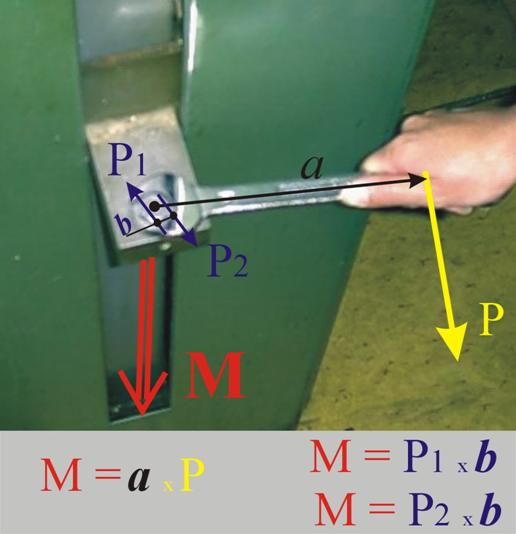
Нека да разгледаме една проста техническа операция - завъртане на гайка с гаечен ключ, както е показано на фиг.1. Върху гаечния ключ са приложени две сили (активната сила от ръката и реакцията на гайката). Тези сили са равни по големина, с успоредни директриси и взаимно-противоположни посоки, така че като ги съберем, ще се получи Р1+Р2=0 - няма равнодействаща. Въпреки това, както може би сте наблюдавали, гаечният ключ не остава в покой. Движението което извършва той е завъртане около неподвижната ос на гайката. За анализиране на такова движение е необходимо да бъде въведено ново понятие - момент на сила.

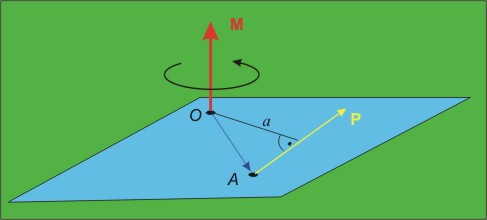
Момент на сила спрямо точка

Фиг.2

По дефиниция моментът на силата Р спрямо точка О се представя от вектора, определен от векторното произведение на радиус-вектора OA и силата Р (фиг.2 и фиг.3).

със следните характеристики:

• приложна точка – точката О

• направление, перпендикулярно на равнината, определена от вектора OA и силата Р

• посока, дадена от правилото за десния винт

• големина ( a е ъгъла между силата и ОА)

Предполагам, че с правилото за десния винт сте се срещал вече изучавайки физика и електротехника като правило, свързано с палеца и свитите пръсти на дясната ръка. За разглеждания случай на фиг.2 може да се каже още, че ако гледаме срещу положителната посока на момента (в случая отгоре), силата ще завърта равнината в посока, обратна на часовниковата стрелка .

Фиг.3

Фиг. 4

Моментът на сила спрямо точка има следните свойства:

• Строго фиксирана посока и големина

• Ако променим посоката на силата, се мени и посоката (знакът) на момента (фиг.3 и фиг.4)

• Когато точката, за която се определя моментът се намира върху директрисата на силата, моментът е нула

• Измерението на момента е [сила х разстояние], най-често [N.m]

• Големината на момента може да се дефинира и като произведение на сила по рамо (Р.а), където рамото а е дължината на перпендикуляра, спуснат от точката към направлението на силата (фиг.2 и фиг.4)

• Ако плъзгаме силата по нейната директриса от една приложна точка до друга, моментът не се изменя, тъй като не се изменя нито рамото а, нито посоката на въртене

Момент на сила спрямо ос

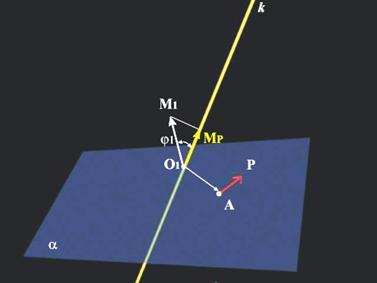
По дефиниция моментът на силата Р спрямо оста к е скаларна величина и е равен на проекцията на момента на силата спрямо коя да е точка от оста върху самата ос.

Фиг. 5

Например, ако това е т.О₁ от фиг.5, първо намираме големината на момента на силата Р спрямо тази точка

После прекарваме равнина a през силата и точката, за да определим направлението на момента М₁ (нормално на a) и ъгъла j1.

Сега можем да проектираме М1 върху к -

Мр е момента на силата Р спрямо оста к.

Фиг. 6

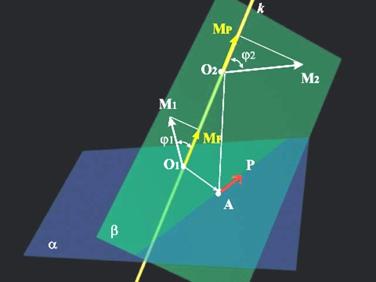
Ако изберем друга точка, например т.О₂, така че

то ще получим по-голям момент -

От друга страна се получава

и ,

така че крайният резултат е същият:

Фиг. 7

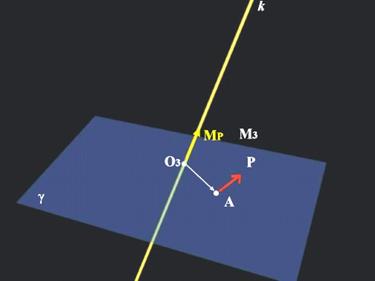
На практика моментът на сила Р спрямо оста к се определя по следният начин (фиг.7) :

През силата се прекарва равнина g, перпендикулярна на оста и се работи с момента на силата спрямо пробода на оста и равнината ( в случая М₃ за т.О₃).

Тъй като по дефиниция и , то моментът съвпада по направление с оста и се проектира върху неко с пълната си големина:

,

или проблемът се свежда до намиране на момент на сила спрямо точка.

При решаване на равнинни задачи, когато силите лежат в една равнина (например равнината на черната дъска), моментът на силите стпрямо третата ос също се отъждествява с момент на сила спрямо точка.

Фиг.8

В случая, показан на фиг.8, всички сили лежат в равнината XАZ (т.А е началото на координатната система. Да намерим момента спрямо оста У е същото, като да намерим момента спрямо т.А.

М_У = М_А

Фиг. 9

За схемата на фиг. 9 М_У = М_В

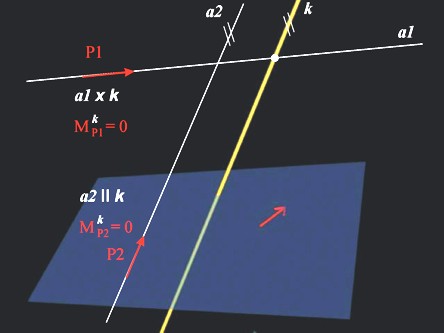
Моментът на сила спрямо ос е нула когато (фиг.10)

• направлението на силата пресича оста, както силата Р₁ и оста к -

• направлението на силата е успоредно на оста, както силата Р₂ и оста к -

Двоица

Фиг. 11(щракнете тук за анимация)

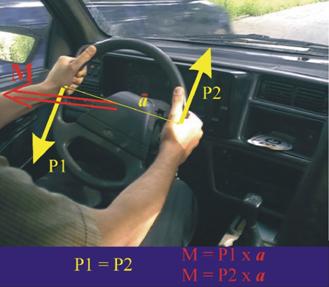
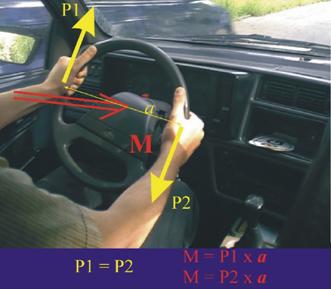
Двоица сили се нарича системата от две равни по големина (Р1=Р2=Р), успоредни по направление и с противоположни посоки сили.

Такива са например силите, с които водачът въздейства на волана при управлението на автомобила, както е показано на фиг. 11.

Главният момент на двоицата е с направление, перпендикулярно на равнината, в която действат силите и с посока, определена от правилото на десния винт.

Големината на главният момент е , къдено а е рамо на двоицата (разстоянието между успоредните директриси на силите)

Фиг. 12

Главната сила на тази система е нула (няма равнодействаща) - .

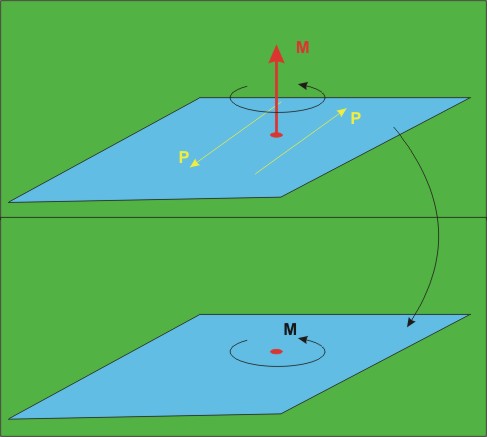
По такъв начин двоицата се характеризира само с момент.

При решаване на задачи в които има действие на двоици, те ще бъдат изобразявани не с двете сили или с вектора-момент, а с насочена дъга, която ще показва посоката на въртене на момента, както е показано на фиг. 12.

Фиг. 13

Ако гледаме срещу положителната посока на вектора-момент, двоицата върти обратно на часовниковата стрелка (фиг.11 и фиг. 13)

Фиг.14

Приложната точка на моментовия вектор може да бъде коя да е точка от пространството, тъй като моментът на двоицата е един и същ за всички точки.

В случая с гайката и гаечния ключ (фиг. 14), двоицата сили, които създават въртящия момент, действат в две срещулежащи точки (два срещулежащи ръба на гайката), а приложната точка на момента се приема в центъра на гайката.

НАТАТЪК