Условия за равновесие на сходяща система
от сили
Според втория закон на Нютон, който
навярно си спомняте от Физика І-ва част, която вече сте минали, ако на един
материален обект действа сила, той ще се движи с някакво ускорение. От тук
следва, че за да бъде в равновесие (ако сте
забравил какво означава това, припомнете си тук), за материалния обект
трябва да е изпълнено:
-
Върху
него да не действат сили. Такъв обект наричаме "изолиран" и той не е
обект на нашето внимание.
-
Равнодействащата
на силите, които действат върху него, да е нула (големината да е равна на
нула). Този случай ще бъде анализиран по-нататък.
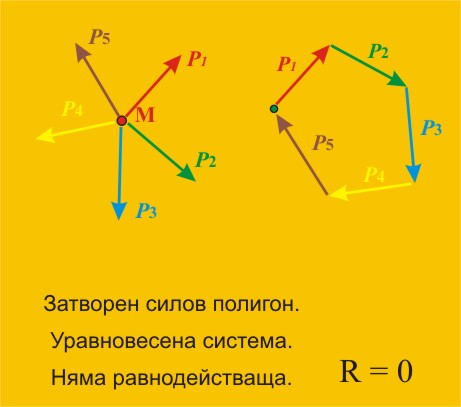
|
Фиг. 17 |
При графичната редукция, за да бъде равнодействащата нула, трябва
последователното нанасяне на силите (началото на всяка следваща сила да е в
края на предишната, ако сте забравил как се
прави графична редукция, щракнете тук) трябва да ни доведе до същата точка,
от която сме започнали ·.
В този случай полигонът се нарича “затворен” или "сключен". Такъв
полигон е изобразен на фиг. 17.
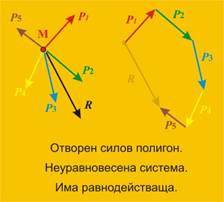
|
Фиг. 18 |
Ако силовият полигон не е затворен,
това означава че системата не е уравновесена
и има равнодействаща ·(фиг. 18).
При аналитичната редукция, за да бъде равнодействащата нула,
трябва всяка от трите й проекции да бъде равна на нула. За пространствения
случай на пет сили условията изглеждат така (ако сте забравил защо, припомнете
си тук):
Rx = Р1х+Р2х+Р3х+Р4х+Р5х = 0
Ry = Р1y+Р2y+Р3y+Р4y+Р5y = 0
Rz = Р1z+Р2z+Р3z+Р4z+Р5z = 0
Като въведем обобщаване за п
на брой сили и символа за сумиране S, аналитичните условия за равновесие на
пространствена сходяща система сили добиват вида:
Rx = 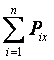 = 0 ,
= 0 ,
Ry = 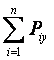 = 0 ,
= 0 ,
Rz = 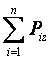 = 0 .
= 0 .
За равнинна система сили, разположена в координатната равнина
хОу, условията за равновесие ще бъдат:
Rx = 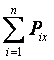 = 0 ,
= 0 ,
Ry = 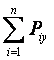 = 0 ,
= 0 ,
а ако е разположена в равнината xOz:
Rx = 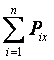 = 0 ,
= 0 ,
Rz = 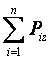 = 0 .
= 0 .
Ако срещате
тези формули за първи път, сега те може да Ви изглеждат чужди. Но ако
посещавате редовно аудиторните занятия и самостоятелно работите варху задачите,
които се решават с тях, ще видите, че те всъщност са много лесни за приложение
(в края на краищата - това са само две уравнения). Тук може да
проследите решението на един такъв пример. За целта ще ви е
необходима програмата Acrobat Reader, инсталация за която
можете да изтеглите тук.