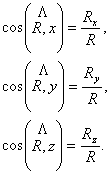Конкурентна (сходяща) система от сили

Анализа на условията за равновесие ще започнем с най-простия материален обект - материалната точка. Както вече беше казано (и друг път ще употребявам "казано" вместо "написано", за което се извинявам), когато точката е изолирана, тя се намира от самосебе си в това състояние, което дефинираме като "равновесие" (какво беше то - ако сте забравили, припомнете си тук). За нас ще представлява интерес случая, когато точката не е изолирана, а влиза във взаимодействие с други материални обекти. Това означава, че тя ще бъде подложена на действието на система от сили. Очевидно е, че те ще имат обща приложна точка (точката която разглеждаме). Исторически, за такава система са се наложили две определения - "конкурентна" и "сходяща". Вие може да употребявате и двете, но за да няма объркване, по-нататък ще използвам само "сходяща". Освен това, за опростяване, ще предполагам, че силите се намират в една равнина (равнинна система сили).

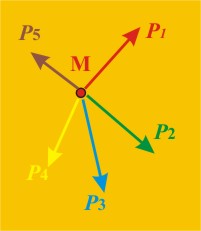
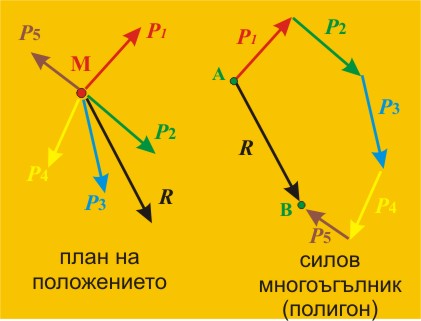
Фиг. 10

И така, предполагаме, че в дадена материална точка М действа равнинна система от п на брой сили (при п=5 се получава случай, изобразен на фиг. 10). Нека си поставим за цел да извършим редукция на системата (какво беше то - ако сте забравил, припомнете си тук). Редукциятя можем да извършим, като използваме позволени операции със силите. В случая ще използваме събиране на две сили.

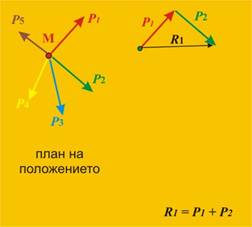
Фиг. 11 (щракни тук за анимация)

Първо ще съберем силите Р₁ и Р₂. Резултатът е силата R₁ (фиг.11):

R₁ = Р₁ + Р₂ (1)

(ако сте забравил как се събират сили - щракнете тук)

Тук и понататък векторните величини ще бъдат означавани с удебелени и наклонени букви.

Фиг. 12 (щракни тук за анимация)

След това събираме новополучената сила R₁ със силата Р₃.

Резултатът е силата R₂ (фиг. 12).

R₂ = R₁ + Р₃ (2)

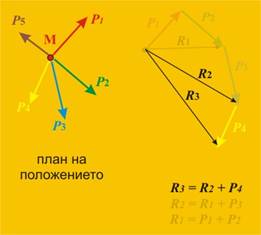
Фиг. 13 (щракни тук за анимация)

Продължаваме с новополучената сила R₂ със силата Р₄.

Резултатът е силата R₃ (фиг. 13).

R₃ = R₂ + Р₄ (3)

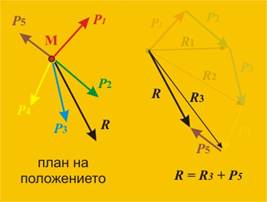
Фиг. 14 (щракни тук за анимация)

Накрая събираме R₃ и последната сила. Резултатът е силата R. Тази сила е еквивалентна по действие на първоначалната система сили (как се нарича такава сила? ако сте забравил, щракнете тук).

R = R₃ + Р₅ (4)

Като се заместят изразите от уравнения 1, 2 и 3 в уравнение 4 ·, окончателно се получава:

R = P₁ + Р₂ + Р₃ + Р₄ + Р₅

Описаната процедура пряко илюстрира графичната редукция на системата. Ето едно обобщение:

Графична редукция

Необходимо е да се разполага с чертеж (план на положението), представящ взаимното разположение на силите в определен мащаб.

С начало в произволна точка А се нанасят силите последователно, като всяка сила започва от върха на предната.

Краят (върхът) на последната сила определя т.В. Векторът R с начало в т.А и край в т.В отговаря на търсената равнодействаща.

Планът на положението изобразява силите с техните направления и посоки, големините на силите трябва да са известни в нютони.

Силовият многоъгълник изобразява последователността на графичната редукция.

Мащабът определя на колко нютона отговаря 1см дължина на вектора в силовия многоъгълник.

Фиг. 15

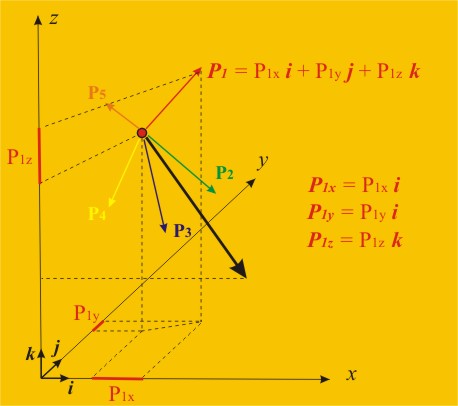
Горната процедура е изградена върху правилата за събиране на вектори. Една от целите, които си поставихме обаче, беше да се създаде методика, която да позволява задачите на статиката да се решават с числа и калкулатор. Това е възможно, ако силите бъдат представени като скаларни величини. За целта въвеждаме правоъгълна координатна система Oхуz, по осите на която има дефинирани единични вектори i, j и k, както е показано на фиг. 15.

Всяка сила може да се разложи по направленията на трите координатни оси (ако сте забравил как става това - щракнете тук за да си припомните).

Например за силата Р₁ получаваме ·:

Р₁ = Р_1х + Р_1у + Р_1z

Всяка компонента пък можем да представим като произведение от дължината на проекцията й върху съответната ос (това е число и дава големината на силата) и единичния вектор на тази ос (това дава направлението и посоката). Например за силата Р₁ това изглежда така:

Р_1х = Р_1x i ·;

Р_1y = Р_1y j ·;

Р_1z = Р_1z k ·,

или като заместим компонентите в горния сбор, се получава ·:

Р₁ = Р_1х i + Р_1y j + Р_1z k , съответно за останалите сили:

Р₂ = Р_2х i + Р_2y j + Р_2z k

Р₃ = Р_3х i + Р_3y j + Р_3z k

Р₄ = Р_4х i + Р_4y j + Р_4z k

Р₅ = Р_5х i + Р_5y j + Р_5z k

Като се съберат равенствата и се изнесат общите множители i, j и k, се получава израза

Р₁+Р₂+Р₃+Р₄+Р₅ = (Р_1х+Р_2х+Р_3х+Р_4х+Р_5х) i +

(Р_1y+Р_2y+Р_3y+Р_4y+Р_5y) j +

(Р_1z+Р_2z+Р_3z+Р_4z+Р_5z) к

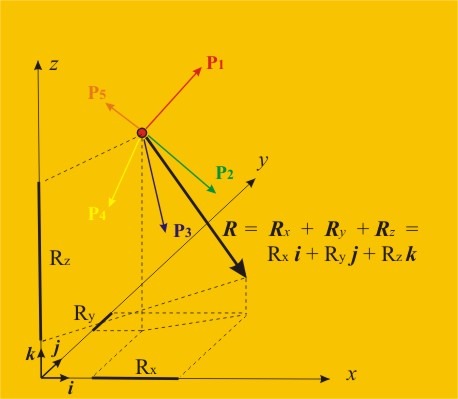
Фиг. 16

Лявата страна на равенството дава търсената равнодействаща R, която също може да бъде разложена по трите оси, както е показано на фиг. 16 ·:

R = R_x+R_y+R_z= R_x i + R_y j + R_z k .

Като обобщим, се получава

R_x i + R_y j + R_z k = (Р_1х+Р_2х+Р_3х+Р_4х+Р_5х) i +

(Р_1y+Р_2y+Р_3y+Р_4y+Р_5y) j +

(Р_1z+Р_2z+Р_3z+Р_4z+Р_5z) к

В това равенство множителите пред i, j и k трябва да са равни, от където се получават три уравнения

R_x = Р_1х+Р_2х+Р_3х+Р_4х+Р_5х

R_y = Р_1y+Р_2y+Р_3y+Р_4y+Р_5y

R_z = Р_1z+Р_2z+Р_3z+Р_4z+Р_5z

Това са изразите за аналитична редукция на сходяща система сили, с помоща на които можем да получим проекциите на равнодействащата по три оси на правоъгълна координатна система. Както сте научили вече от аналитичната геометрия, пълната големина на равнодействащата ще получим така:

,

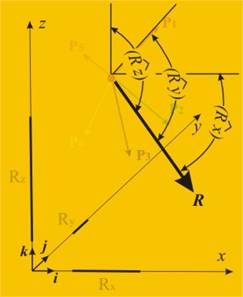
а направлението и посоката могат да се определят с ъглите показани на фиг.17, които равнодействащата сключва с трите координатни оси:

Фиг. 17

Нататък