Аксиоми на статиката
Статиката е раздел от
Теоретичната механика, в който се изучават условията, при които едно идеално
твърдо тяло, материална точка или материална система са в равновесие. Това означава тялото да запазва състояние на покой или на праволинейно равномерно
движение.
От физиката навярно
знаете, че всяка материална точка (или тяло), която е изолирана (не си
взаимодейства с други точки), се намира в равновесие. За нас интерес
представляват материалните обекти, които не са изолирани и са подложени на
външни въздействия. Това предполага наличието на сили, приложени върху точката
като мярка на взаимодействието.
|
Фиг. 5
Фиг. 6 |
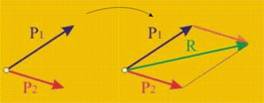
Ако дадена
система сили е приложена върху материална точка, и тя остава в покой или
извършва равномерно праволинейно движение, казваме, че силите от системата
взаимно се уравновесяват или са в равновесие. Нашата цел тук е да изведем уравнения, с които да пресметнем
дали дадена известна система сили е в равновесие (първа основна задача -
знаем силите, проверяваме дали системата е еквивалентна на нула, фиг.5), или да пресметнем
неизвестни сили от уравновесена система сили (втора основна задача - знаем, че
системата е еквивалентна на нула, търсим някои сили които са неизвестни, фиг.6). Всички уравнения на
статиката се извеждат от няколко изходни положения (аксиоми), които се приемат
без математическо доказателство, на основата на опита и наблюдението на
действието на силите върху материалните обекти. Тук ще бъдат изложени само тези аксиоми,
които пряко се използват в по-нататъшните изводи.
|
Фиг.7 |
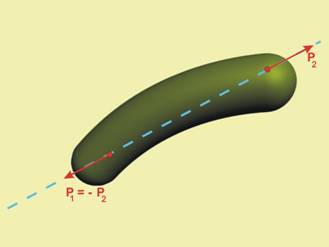
Две сили, приложени върху идеално твърдо тяло се уравновесяват тогава и
само тогава, когато (фиг.7):
1. Имат обща директриса
2. Имат противоположни посоки
3. Имат равни големини
Първата аксиома определя най-простата
уравновесена система сили.
Ако към дадена система сили, приложена към идеално
твърдо тяло, прибавим или премахнем уравновесена система сили, кинематичното
състояние на тялото не се променя.
Действието на
тази аксиома се илюстрира при доказателството на следното следствие:
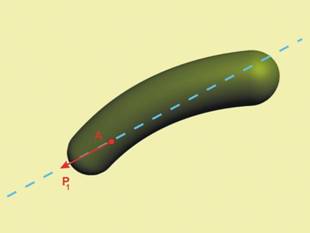
Ако една сила действа върху идеално твърдо тяло,
можем да я плъзнем по нейната директриса до друга приложна точка без да
променим кинематичното състояние на тялото (действието на силата върху тялото остава
същото).
|
|
1.
Разглеждаме силата Р1, приложена в т.А на идеално твърдо
тяло
|
|
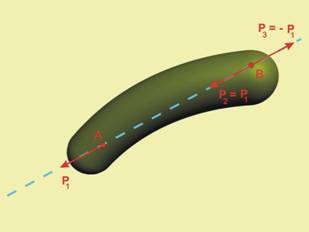
2.
В т.В от директрисата на силата Р1 прилагаме уравновесена
система от две сили - Р2 и Р3, равни по големина на силата Р1.
Съгласно аксиомата, кинематичното състояние на тялото не
се изменя ·.
|
|
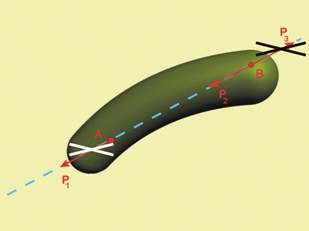
3.
Забелязва се, че се е формирала нова
уравновесена система от две сили - Р1 и Р3. Според втората
аксиома, кинематичното състояние на тялото няма да се промени, ако премахнем
действието на тази система ·.
Това и правим ·!
|
|
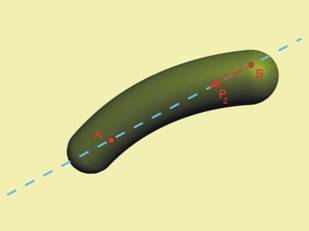
4.
В резултат на двукратното използване на
аксиомата (първо приложихме, а после премахнахме уравновесена система сили),
остана да действа само силата Р2, която отговаря на силата Р1, но плъзната в
т.В.
Трета аксиома
Ако две сили имат обща приложна точка, то те могат да се
заменят с една сила (равнодействаща), приложена в същата точка и равна на
геометричния им сбор (по големина и направление съвпада с диагонала на успоредника, построен
от тези сили, фиг.9)
|
Фиг.9 |
R = P1 + P2
P1 и P2 се събират
като вектори ·.
Посоката на
равнодействащата R трябва да е както е показана на схемата - Р1
и Р2 "се гонят", а R трябва да "ги пресреща".
Тази аксиома е известна още като "правило
на паралелограма".
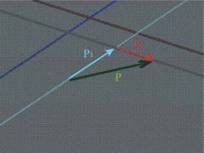
Трета аксиома може да се разглежда като правило за събиране
на сили. При решаване на задачи често се налага да бъде извършвана обратната
процедура - при дадена сила и две произволни направления, силата да бъде
заменена с еквивалентна система от две сили, директрисите на които да са
успоредни на дадените направления (фиг.10). Или както често се казва - силата да бъде разложена по двете направления. Графично решението изглежда както на фиг. 9 и се провежда
в следната последователност:
|
|
1. Едното направление се плъзга успоредно,
докато съвпадне с началото на силата (в случая това е синьото направление, а
силата е Р)
|
|
2. Второто направление се плъзга успоредно,
докато съвпадне с края на силата (в случая това е червеното направление);
|
|
3. Двете нови страни на получения триъгълник са търсените
сили. Посоките поставяме, като спазваме същото правило, както при събирането ·.
Не трябва да се забравя, че двете нови сили
трябва да бъдат приложени в същата точка, както и изходната ·.
На практика най-често се налага да разлагаме
сила по две взаимно-перпендикулярни направления, успоредни на координатните
оси. Това изглежда така:
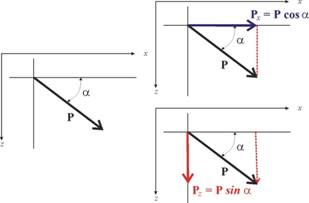 или така:
или така: 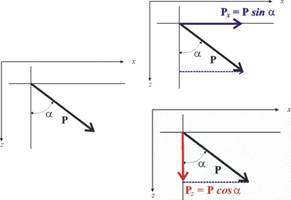
Четвърта аксиома (принцип на действието и
противодействието)
Две материални тела си взаимодействат винаги с две
противоположни сили (сили с една директриса, противоположни посоки и равна
големина). Тези сили се наричат "действие и противодействие".
|
|
·
Тялото В
действа на тялото Е със сила РВЕ.
·
Същевременно и тялото Е действа върху тялото В
със сила РЕВ.
·
Силата РЕВ
е противоположна на силата РВЕ
, или РЕВ = -РВЕ
Двете сили действат върху различни тела. Затова, въпреки че са
противоположни, те не се уравновесяват.
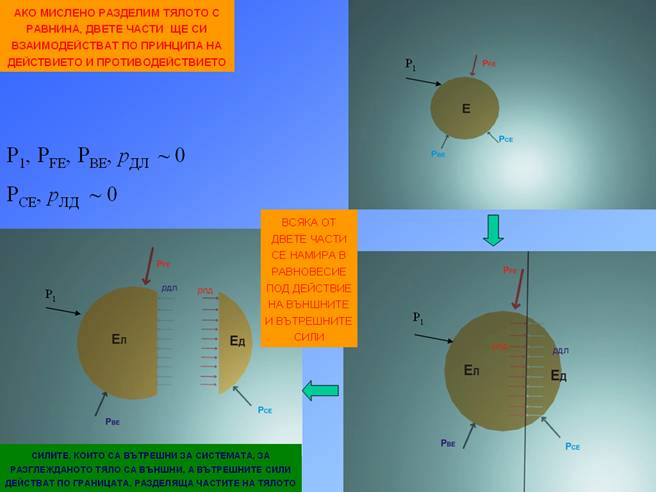
Пета аксиома (принцип на локалното равновесие)
Ако едно тяло е част от механична система, която се намира в
равновесие под действието на някакви външни сили, то тялото отделено от
системата щи се намира в равновесие под действието на външните и вътрешните сили.
Външни за една материална система са силите, с които телата от системата взаимодействат с тела
извън системата.
Вътрешни са силите, с които телата от системата взаимодействат
помежду си.
Външни за едно материално тяло са силите, с които то взаимодейства с други тела.
Вътрешни са силите, с които частичките, които изграждат тялото взаимодействат
помежду си.
|
|
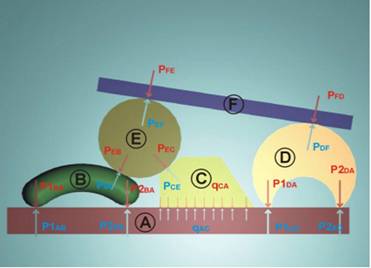
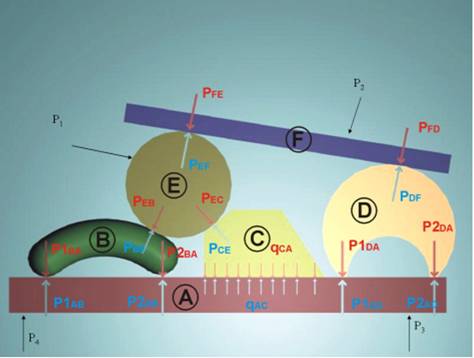
За показаната механична система, силите Р1, Р2, Р3
и Р4 са външни.
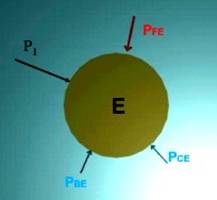
Тялото Е трябва да се намира в равновесие под действието на външната сила Р1
и вътрешните сили РВЕ, РСЕ и РFE.
Р1, РВЕ, РСЕ, РFE ~ 0
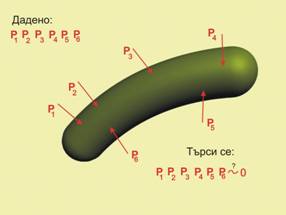
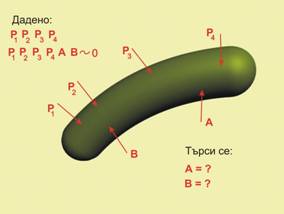
Принципът на локалното равновесие
важи и за частите на тялото. Ако едно тяло се намира в равновесие под
действието на външни сили, то всяка негова част се намира в равновесие под
действието на външните и вътрешните сили:
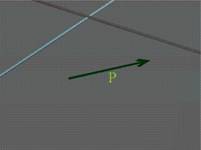 Фиг.10
Фиг.10