ТЕОРЕМА ЗА КИНЕТИЧНИЯ МОМЕНТ НА МАТЕРИАЛНА ТОЧКА

 

Задача №1   Топче на нишка   (стр.175 от [4])

 

Условие:

 

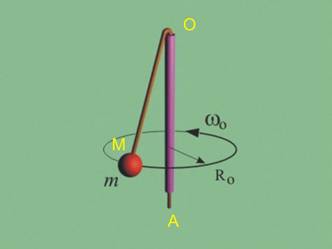
Фиг.1   ·

Сачмата М е завързана към шнура МОА (фиг.1), който минава през вертикална тръба. Сачмата обикаля около тръбата по окръжност с радиус R0 и прави 120 оборота в минута ·.

Через бавно издърпване на шнура се скъсява частта му вън от тръбата ·, така че сачмата да описва окръжност с радиус R=0.5Ro ·.

Да се определи колко оборота в минута прави сачмата при това ново положение.

 

 

 

Решение:

Задачата ще бъде решена с помощта на теоремата да кинетичния момент:

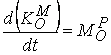, като уравнението от теоремата проектираме върху оста на въртене (оста z от фиг.2).

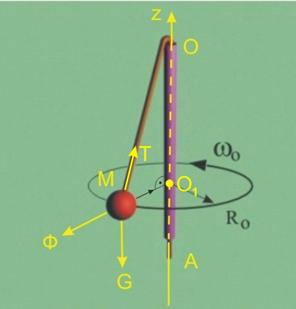
Фиг.2

По време на движението, върху сачмата действат три сили.  

-         Сила на тежестта G. Тази сила е успредна на z ,така че моментът ще бъде нула:  MzG=0.

-         Инерционна сила Ф. Тази сила пресича z в т.О1, така че моментът ще бъде нула:  MzФ=0.

-         Опънна сила Т в нишката. Тази сила пресича z в т.О, така че и нейният момент ще бъде нула:  MzТ=0.

От анализа на силите се вижда, че моментът на действащите сили е нула: MzР = MzG + MzФ + MzТ = 0,

и в този случай действа теоремата за запазване на кинетичния момент:

          .

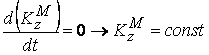Ако фиксираме два момента от движението -  преди изтегляне на нишката и ‚ след изтегляне на нишката, от получения израз следва, че кинетичните моменти в двата случая са равни:

К = К‚ .

Кинетичните моменти ще бъдат определени за дсяко положение по отделно (фиг.3):

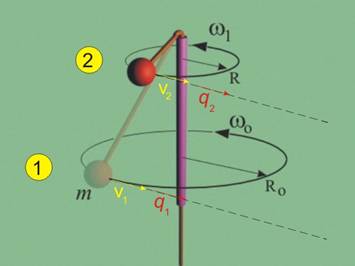
Фиг.3

-         Положение   - сачмата се върти по окръжност с радиус R0 с ъглова скорост wo, която формира линейна скорост

v0 = R0 wo. Кинетичният момент се получава:

К = R0 v0 = R02 wo.

-         Положение ‚  - сачмата се върти по окръжност с радиус R1 с ъглова скорост w1, която формира линейна скорост

v1 = R1 w1. Кинетичният момент се получава:

К‚ = R1 v1 = R12 w1.

Като приравнин двата кинетични момента:

R02 wo = R12 w1 ,

за неизвестната ъглова скорост се получава ,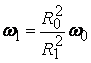

и като се вземе пред вид, че по условие R1 = 0.5 R0 :

.

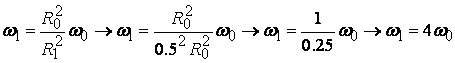Същото отношение важи и за техническите ъглови скорости (тези, които се мерят с обороти за минута и се отбелязват със символа n):

n1 = 4 n0.

По условие  n0 = 120 об/мин , така че окончателно за неизвестната скорост се получава:

n1 = (4) (120) = 480 об/мин.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ПРОДЪЛЖИ >>>