Основно уравнение на динамиката на материална точка. Принцип на Даламбер.

В темите от раздел "Статика" разгледахме условията за равновесие на телата под действие на система от сили. В раздел "Кинематика" рагледахме движението на телата и някои случаи на определяне на скорости и ускорения. С тази тема започва нов раздел - "Динамика", чиито предмет е изучаване на движението на телата и формирането на скорости и ускорения под действие на приложените сили. При анализа на движението, какъвто ще бъде направен тук, ще бъдат изведени формули, позволяващи решаването на следните два вида задачи:

- При известно движение на материалния обект да бъдат определени силите, предизвикващи това движение.

- При известни сили, действащи върху материалния обект, да бъде определен законът на движението му.

Както в другите два раздела на Теоретичната механика, и тук анализа ще започнем с материална точка. Основният инструмент, който ще бъде използван, е известният Ви (надявам се) от физиката Втори закон на Нютон (основен закон на динамиката):

Фиг. 1 ·

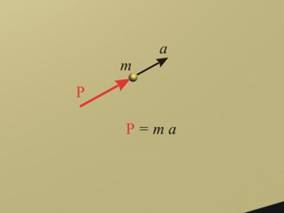
Големината а на ускорението на дадена точка е право-пропорционално на силата Р, която действа върху нея и обратно-пропорционално на нейната маса т (фиг.1).

или Р=та.

За да се придаде на дадена точка определено ускорение а, колкото по-голяма маса има точката, толкова по-голяма трябва да бъде силата.

Фиг. 2 ·

Върху телата, които се намират в обхвата на гравитационно поле, действа сила на тежестта, насочена към центъра на привличане.

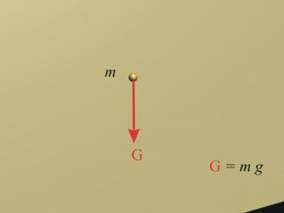
Близо до земната повърхност силата на земното привличане G (на тежестта) се възприема насочена вертикално надолу (фиг.2).

Ускорението, което придобиват телата под действие на силата на тежестта е g≈9.81 m/s2

g≈9.78 m/s2 на екватора, g≈9.83 m/s2 на полюса, при нулева надморска височина

Фиг. 3

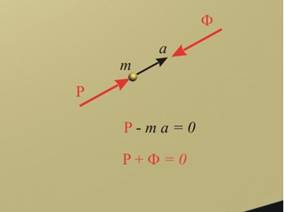
Движението на материална точка с ускорение а поражда инерционна сила

Ф = -ma

с направление и големина както на силата Р, която поражда движението, но с противоположна посока .

Основното уравнение може да бъде преработено така, че в дясно да остане 0 :

Р - та = 0.

Като се замести инерционната сила Ф по определение, получава се уравнение за равновесие на системата сили Ф и Р:

Р + Ф = 0.

Полученото уравнение може да бъде тълкувано по следния начин (Принцип на D’Alembert):

Ако към силата, действаща върху точката, се приложи и инерционната сила, получената система ще бъде в равновесие.

С помощта на принципа на D’Alembert всяка задача от динамика на точка може да се реши с методите на статиката, тъй като задачата се свежда до равновесие на сходяща система сили.

Действието на принципа на ще бъде илюстриран със следните примери :

r Вертикално движение на платформа (асансьор) ·.

r Движение на водата в речно корито ·.

r Движение на тежести от ротационен маховик ·.

и задачи:

r Определяне на сила, действаща върху точка с известно движение ·

r Определяне на характеристиките на движението на точка при известна сила, действаща върху нея. ·