r ДВИЖЕНИЕ НА ТЕЖЕСТИ ОТ РОТАЦИОНЕН МАХОВИК

Фиг. 1

Фиг. 2 ·

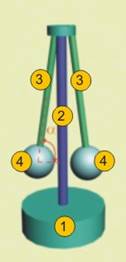
Нека да разгледаме ротационен маховик, състоящ се от основа , ос‚, две рамена ƒ и две ротационни тела „(фиг.1).

Когато маховикът е в покой, върху ротационните тела действа само силата на тежестта. Под действие на тази сила рамената на маховика са прибрани и ъгълът a между оста и хоризонталното направление е близък до 90^о.

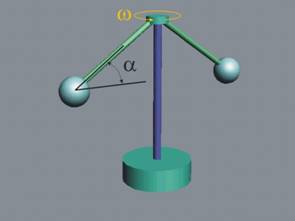
Ако маховикът се завърти с постоянна ъглова скорост w, върху ротационните тела започват да действат инерционни сили, които разтварят рамената и ъгълът a става по-малък (фиг.2). За работата на маховика е необходимо да се познава зависимостта на ъгъла от ъгловата скорост w.

Фиг. 3

Фиг. 4

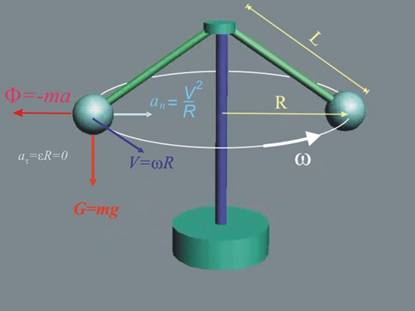
Първо да проследим формирането на инерционната сила (фиг.3).

Тъй като условието беше маховикът да се върти с постоянна ъглова скорост w, ъгловото ускорение e ще е нула, поради което тангенциалната компонента a_t на ускорението на ротационните тела също ще е нула:

a_t = eR = 0

Пълното ускорение а обаче няма да е нула, тъй като ще има нормална компонента:

.

Така инерционната сила ще има големина

Ф = та

и ще бъде насочена навън (обратно на посоката на ускорението), както е показано на фиг.3.

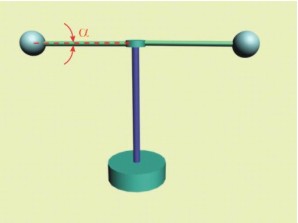
По време на движението всяко от ротационните тела трябва да се намират в равновесие под действието на силата на тежестта G, инерционната сила Ф и реакцията по оста на рамото Т (фиг.4):

.

В DАВС дължината на хипотенузата АС ще отговаря на големината на силата Т, а дължината на катетите - на другите две сили. Тогава за ъгъла ще се получи

.

Като вземем предвид зависимостите

,

получаваме връзката между тангенса на ъгъла и ъгловата скорост:

.

Понякога анализът на връзката между скоростта на въртене и ъгълът на отклонение на рамената на маховика се провежда по удобно, ако разполагаме с израз за синуса от ъгъла. Такъв израз може да се получи, като заместим радиуса R с дължината на рамото, изразена от DDAO ® .

От друга страна . Като съпоставим двата израза за tg(a), получаваме:

.

Фиг. 5

Фиг. 6

След като разполагаме с формули за определяне на ъгъла на отклонение на рамената, можем да преминем към анализ на самото движение.

Когато маховикът забавя движението си и спира, тогава ъгловата скорост w клони към нула и се получава:

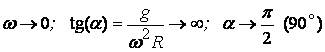(фиг.5).

Когато маховикът ускорява движението си и започва да се движи с много голяма ъглова скорост w, клоняща към безкрайност, се получава:

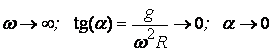(фиг.6).

Зависимостта на ъгъла от скоростта на въртене може да бъде илюстрирана със следната таблица:

w1 < w2	w2	w3 > w2
, sin(a1) > sin(a2), a1 > a2		, sin(a3) < sin(a2), a3 < a2