ЗАДАЧА №1 Определяне на сила действаща върху точка, чието движение е известно

Условие:

Точка с маса т се движи в равнина под действие на силата Р по следния закон:

х = 3 sin( p t ) ; y = 5 cos( p t).

Да се определи силата, предизвикваща движението

Решение:

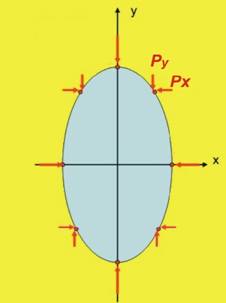
Фиг. 1

Като подготовка на решението, първо ще определим траекторията, по която се движи точката. За целта ги преработваме така, че от едната страна на равенството да остане само тригонометричният израз: ,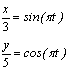

вдигаме двете уравнения на квадрат: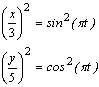

и събираме левите и десните страни. Двете суми трябва да са равни:

Понеже sin²( p t ) + cos²( p t) = 1, то окончателно за траекторията получаваме:

- уравнение на елипса.

Решението на задачата и намирането на компонентите Рх и Ру на силата се провежда за всяка ос поотделно (фиг.1) . За прегледност, решението е подредено в таблица.

	По х	По у
1. Основното уравнение на динамиката ma = P се проектира по двете оси:	m ax = Px	m ay = Py
2. Компонентите на ускорението се опеделят через двукратно диференциране на закона на движението:	х = 3 sin( p t ) Vx = = 3 cos(p t ) ; ax = = -3 sin(p t )	y = 5 cos( p t) Vy = = -5 sin(p t ) ay = = -5 cos(p t )
3. Заместване на получените компоненти на ускорението в основното уравнение на динамиката	Px = - 3 m sin(p t ),	Py = - 5 m cos(p t )

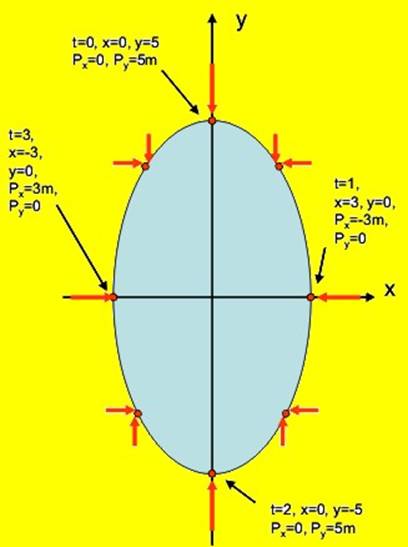
Фиг. 2

Силата може да бъде описана с компонентите си в някои характерни моменти от движението (t=0; t=1s; t=2s; t=3s и т.н., Фиг.2)·.

Като разполагаме с компонентите по двете оси, за всеки момент може да бъде определена и пълната големина на силата по формулата ·.