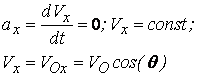ЗАДАЧА №2
Определяне на характеристиките на движението на точка при известна сила,
действаща върху нея
|
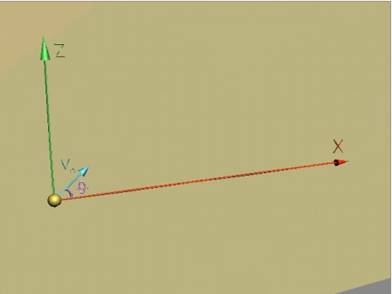
Фиг.1 ·
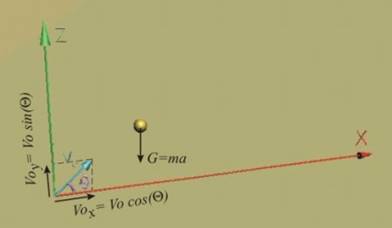
Фиг.2 |
Условие:
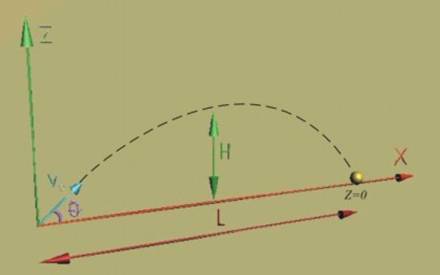
Точка с маса т е хвърлена под ъгъл q ·спрямо хоризонта с известна началната скорост на движението V=Vo·.
Да се определят характеристиките
на движението (скорост, ускорение и закон на движение) и големините на ъгъла,
при които точката ще достигне най-голяма височина или най-голяма далечина на
полета (съпротивителните сили се пренебрегват).
Решение:
За описание на движението се
прекарва координатна система XOZ · с начало в началното положение на точката (Xo=0 и Zo=0, фиг.1).
Единствената сила, която действа
на точката е силата на теглото G (фиг2). Тя е насочена по оста z, така че проекциите на силата, действаща върху
точката ще бъдат Рх=0 и Рz= -G.
Диференциалните уравнения на
движението ще се получат, като основното уравнение та=P се проектира по двете оси:
или 
.
Решението на задачата и намирането на характеристиките на
движението се провежда за всяка ос поотделно. За прегледност, решението е
подредено в таблица.
|
|
По х |
По у |
|
1. С
еднократно интегриране се получават изрази за скоростта: Неизвестните константи
определяме от условието, че при t=0 компонентите на скоростта са известни (виж фиг.2) |
|
|
|
2. С още едно
интегриране се получават изрази за закона на движение: Неизвестните
константи С3 и С4 определяме от условието, че при t=0 точката
се намира в началото на координатната система (виж фиг.2) |
|
|
Анализ на движението
r
Определяне на
височината Н на полета ·
|
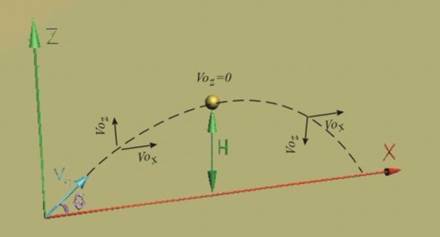
Фиг. 3 · |
Височината на полета ще определим,
като в уравнението на закона на движение по ординатата z заместим времето с
неговата стойност tH в момента, когато точката достига максимална височина.
Момента tH ще определим от условието, че когато
точката достига максимална височина, проекцията на скоростта върху оста у е нула
Заместваме времето tH в уравнението за Z:
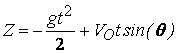® t=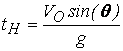
® H=Z ; ® 
.
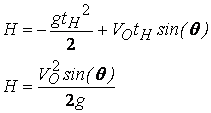r
Определяне на далечината
L на полета ·
|
Фиг. 4 · |
Далечината на полета ще определим,
като в уравнението на закона на движение по ординатата х заместим времето с неговата стойност tL в момента, когато точката отново падне на хоризонталната ос.
Момента tL ще определим от условието, че в началото (t=0) и в края (t=tL) на полета координатата Z е нула (фиг.4).
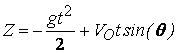
Заместваме времето tL в уравнението за x:
® t =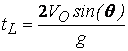
® 
.
Най-голяма стойност L ще има при sin(2q)=1,
или при 
,
от където 
или още q = 45o.
