ПРИМЕР №1
Количка и топче
|
|
Условие:
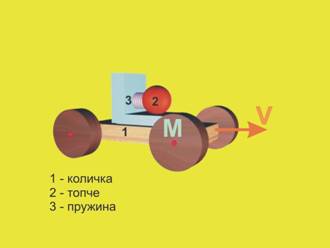
Система от количка,
пружина и сфера с обща маса М=6kg, се движи с
постоянна скорост V=4m/s (фиг.1).
Да се определи скоростта на количката VK, ако след освобождаване на пружината,
сферата с маса тС=1kg добива скорост VC=30 m/s (фиг.2) ·.
Решение:
Ако анализираме
действащите върху системата сили в една правоъгълна координатна система, както
на фиг.2, ще видим, че ако пренебрегнем силите на триене (в условието не е
казано нищо за тях), ще останат сили, действащи само по оста z (силите на тежестта). Скоростта на системата пък е
насочена само по оста х. Така че ако
проектираме уравнението от теоремата за количеството на движението (в
интегирания й вид) върху оста х, тъй
като проекциите (Gk)x=0 и (Gс)x=0 , ще се получи:
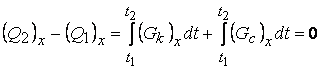 .
.
(Q1)x е проекцията на количеството на
движението в първия момент, преди освобождаването на пружината, когато двете
тела се движат като едно цяло, с еднава скорост V ·. Поради това този член се получава
като:
(Q1)x = М V.
(Q2)x е проекцията на количеството на
движението във втория момент, след освобождаването на пружината, когато двете
тела се движат самостоятелно с различни скорости·. Поради това този член се получава
като:
(Q2)x = тк Vк + тc Vc .
Получените изрази се
заместват в уравнението на теоремата, първо символно:
![]() ® (тк Vк + тc Vc ) - М V = 0,
® (тк Vк + тc Vc ) - М V = 0,
а след това и с числените
стойности от условието (масата на количката се получава като разлика от общата
маса и масата на сферата - тк = 6-1 = 5kg):
5 Vк + (1)(30) = (6)(4),
5 Vк =
24 - 30,
![]() .
.
Отрицателният знак тук
означава, че след освобождаване на пружината количката ще се започне да се
движи в посока, обратна на положителната посока на оста х (в случая - назад).
Ако скоростта на
сферата не беше 30 m/s , а 24 m/s , тогава количката
щеше да спре, а ако беше по-малка от 24 m/s , количката щеше да продължи да се
движи напред, но с по-малка скорост от началната. Доказването на тези две
твърдения на изпита ще Ви даде шанс да получите четворка.
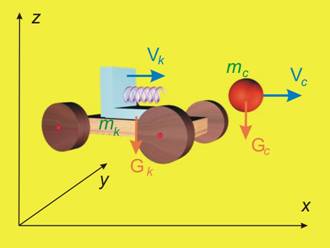 Фиг.2
Фиг.2