КИНЕМАТИКА НА РОТАЦИОННО ДВИЖЕНИЕ НА ТЯЛО

Фиг.1 ·

Фиг.2 ·

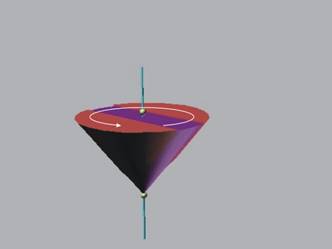
Едно тяло се движи ротационно, когато две точки от него остават неподвижни по време на движението. Двете точки определят една права, която се нарича ос на въртене (ротация, фиг.1). Такова движение извършват много елементи на машините и апаратите - химически бъркалки·, трансмисионни валове·, пластифициращи валяци· и др.

Тъй като тялото остава по време на движението си в едно място от пространството, то за да се познава неговото движението е достатъчно да се познава закона, по който то се върти около оста на ротация. За целта през нея се прекарват две равнини. Едната се приема за неподвижна (свързана например с екрана на монитара), а другата за подвижна, свързана с въртящото се тяло (фиг.2). Нека да приемем, че в началото на движението двете равнини съвпадат, след което тялото започва да се върти. Подвижната равнина ще започне да се върти заедно с тялото, тъй като е свързана с него, и между двете равнини ще се образува ъгъл j·. Този ъгъл определя във всеки един момент положението на тялото. Ако знаем как се изменя този ъгъл във времето, можем да кажем, че познаваме движението на тялото. Или в този случай законът на движение е едно уравнение:

j = j(t).

За положителна посока на въртене се приема посоката, обратна на часовниковата стрелка.

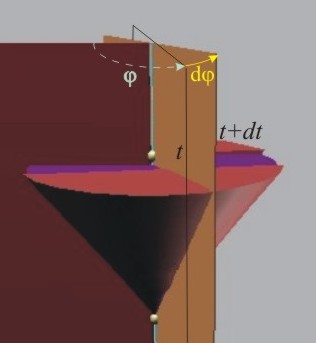
Нека в даден момент положението на тялото се определя от ъгъл j, а след изтичане на време Dt този ъгъл е нарастнал с Dj (тялото се е завъртяло малко в същата посока, фиг.2). Аналогично на понятието средна скорост на преместване, тук можем да дефинираме средна скорост w_cp на изменение на ъгъла (средна ъглова скорост):

.

Ъгловата скорост на тялото се определя като

,

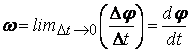т.е като първата производна на закона на движение спрямо времето.

Ако ъгълът се измерва в радиани, то мярката за бързината, с която се изменя ъгълът би трябвало да бъде rad/s. Почти винаги обаче дименсията на ъгловата скорост ще срешнете без радиан като s^-1.

Аналогично на ускорението при линейното движение, което показва бързината, с която се изменя скоростта, при ротационното движение се въвежда ъглово ускорение. Ако за даден интервал от време Dt ъгловата скорост се измени с Dw , бързината, с която се изменя ъгловата скорост може да бъде характеризирана със средното ъглово ускорение [s^-2].

Под понятието ъглово ускорение се разбира

.

Както при линейното движение, и тук според знака на ускорението може да се дефинира ускорително, закъснително и равномерно движение.