СКОРОСТИ И УСКОРЕНИЯ НА ТОЧКИ ОТ ТЯЛО, ИЗВЪРШВАЩО РОТАЦИОННО ДВИЖЕНИЕ

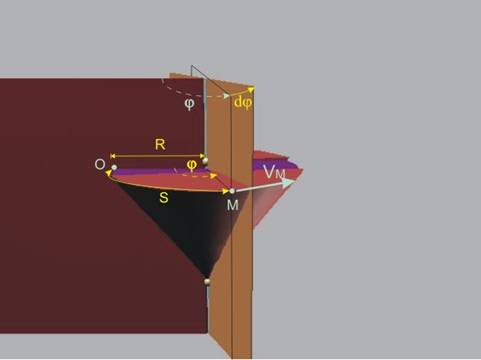
Фиг. 1

Дефинираните в предишните теми величини ъгъл на завъртане (j), ъглова скорост (w) и ъглово ускорение (e), характеризират движението на тялото като цяло. При решаването на редица задачи в областта на техниката се налага да бъдат определяни скоростите и ускоренията на точки от тялото. Един от начините те да бъдат определени е следният:

Да разгледаме тяло, което извършва ротационно движение и т.М от него, отстояща на разстояние R от оста на ротация (фиг.1). При въртенето на тялото около оста на ротация, точката описва окръжност в равнина, перпендикулярна на тази ос. Това означава, че ние познаваме траекторията на точката, и за описание на нейното движение можем да използваме естествен метод. За целта като отправна точка избираме т.О, лежаща върху неподвижната равнина. Положението на т.М се определя от криволинейната координата S, която може да бъде изчислена като дължина дъга с централен ъгъл j.

.

За скоростта V_M на точката може да се каже, че е насочена по допирателната към траекторията (в случая - окръжността) и че може да бъде определена по естествения метод като

,

т.е. големината на скоростта на една точка от ротационно движещо се тяло е равна на произведението от ъгловата скорост на тялото и разстоянието между точката и оста на въртене.

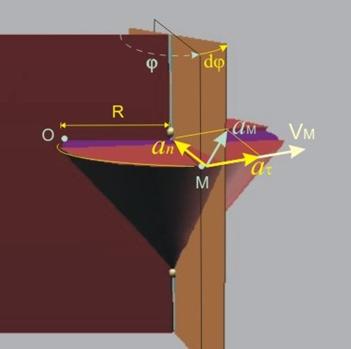
Фиг. 2

При естествения начин на задаване на движението, ускорението се определя с двете си компоненти а_t и а_п (фиг.2).

Тангенциалната компонента а_t съвпада по направление със скоростта V_M и се получава при нейното диференциране:

.

Нормалното ускорение е насочено към цинтъра на въртене и се получава по формулата, известна от кинемотика на точка:

.

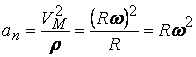Пълното ускорение можем да изчислим по правилото на паралелограма като хипотенуза в правоъгълен триъгълник:

,

или

.