КИНЕМАТИКА НА РАВНИННО ДВИЖЕНИЕ НА ТЯЛО. МОМЕНТЕН ЦЕНТЪР НА СКОРОСТТА.

СКОРОСТ И УСКОРЕНИЕ НА ТОЧКА ОТ ТЯЛОТО.

Едно тяло се движи равнинно, когато всички негови точки остават при движението си в равнини, успоредни на дадена неподвижна равнина.

Фиг.1 ·

Фиг.2

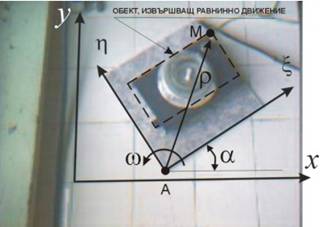
Например точките C и D на основата и корпуса на химическата бъркалка от фиг.1 се движат в различни равнини, намиращи се една над друга, но и двете равнини са успоредни на плота. По време на движението отсечката CD се движи транслационно, така че ако познаваме движението на т.С от основата, може да кажем, че познаваме движението на т.D и на останалите точки от корпуса, намиращи се върху отсечката. Следователно, ако познаваме движението на точките от основата, може да кажем, че познаваме движението на целия корпус.

Такива отсечки могат да бъдат въведени във всяко тяло, което извършва равнинно движение. Тогава, вместо да се разглежда движението на цялото тяло, анализът на движението се съсредоточава върху едно сечение с равнина, успоредна на неподвижната равнина.

За анализиране на движението, с неподвижната равнина (в нашия случай това е плота)се свързва абсолютна (глобална) координатна система хОу, а с подвижното равнинно сечение - местна (локална) координатна система xАh (фиг.2).

Равнинното движение може да се разглежда като съставено от две движения – транслационно и ротационно.

Известно е, че транслационното движение е определено, ако се познава движението на една точка. Нека тази точка да бъде полюсът А с координати х_А и у_А. Тъй като по дефиниция в този случай точката се движи в една равнина, законът на движението ще се дава само от две уравнения: х_А =f₁(t) и у_А =f₂(t).

От друга страна, ротационното движение е определено от ъгъла на завъртане a.

Трите уравнения

х_А =f₁(t),

у_А =f₂(t),

a =f₃(t); (t- време),

представляват законът на движение на тялото. Първите две характеризират транстлационната компонента на движението, а третото – ротационната.

Фиг.3

Скоростта на точка от тялото (например на т.М, фиг.3) се получава като сума от скоростта V_A на полюса (транслационна компонента) и скоростта V^A_M, с която точката се завърта около полюса (ротационна компонента).

V_М = V_A + V^A_M .

Скоростта на завъртане можем да определим както при ротационно движение:

V^A_M = wxr,

така че окончателно се получава

V_М = V_A + wxr.

Ако за полюс А бъде избрана точка, която в дадения момент е неподвижна (V_A=0), то скоростта на т.М се получава само като скоростта wxr на завъртане на точката около полюса – задачата се свежда до задача от ротационно движение. Тази точка от разглежданото сечение на тялото, чиято скорост в дадения момент е нула се нарича моментен център на въртене (моментен център на скоростта). Този подход за определяне на скорости на точки от тялото е много разпространен в техническите анализи. За целта е необходимо да бъде определен моментния център на въртене. Тук ще разгледаме някои характерни случаи.

r Първи случай

Фиг. 4

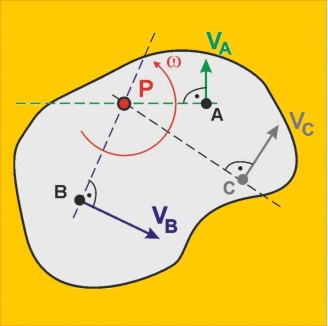
Известни са направленията на скоростите на две точки (т.А и т.В) от сечението, като тези направления не са успоредни помежду си (фиг.4).

Моментния център на скоростите (Р) е пресечницата на перпендикулярите, издигнати от в т.А и т.В към направленията на съответните скорости. Ъгловата скорост на тялото около т.Р може да се определи от формулата за ротационно движение:

w = V_A/РА

или

w = V_В/РВ.

При известна ъглова скорост, скоростта на всяка друга точка С от тялото може да бъде намерена по формулата

V_С = wхРС .

r Втори случай (фиг.5)

Фиг. 5

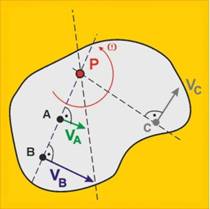
Известно е общото направление на скоростите на две точки (А и В) от сечението, като това направление е перпендикулярно на осечката АВ. Така, ако се опитаме да работим по начина от първи случай, двата перпендикуляра ще се слеят и няма да могат да се пресекат. В този случай е необходимо да познаваме и големините на скоростите V_A и V_В

Моментния център на скоростта е пресечната точка на правата, определена от т.А и т.В с правата, определена от върховете на векторите-скорост. Според посоката на скоростите, т.Р може да се получи между двете точки или от страната на точката с по-малка скорост.

Фиг. 6

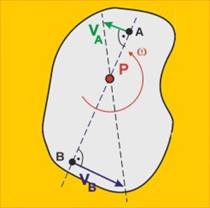
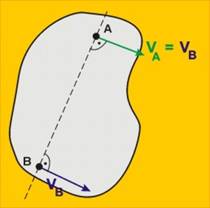
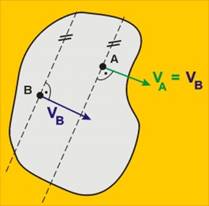
Ако във втория случай скоростите на точките А и В са с еднаква големина или ако скоростите са равни, еднопосочни и успоредни, но точките са разположени така, че перпендикулярите към скоростите не съвпадат, тогава моментния център на скоростта е в безкрайността и тялото извършва транслационно движение.

Фиг. 7

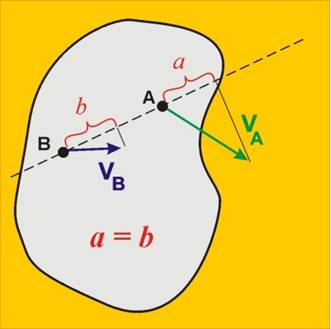
r Теорема за проектираните скорости

Проекциите на скоростите на две точки А и В от разглежданото сечение върху оста, минаваща през точките, са равни (фиг.7).

r Търкаляне без приплъзване

Фиг.8 ·

Един често срещан случай в задачите от кинематика на равнинно движение е търкалянето на корав диск върху равнина без приплъзване. Като пример ще разгледаме движението на колелото от строителна количка (фиг.8). Това колело извършва съвкупност от ротационно движение (върти се около оста си) и транслационно движение (оста се премества успоредно на равнината). Приема се, че то контактува с равнината, по която се търкаля (пода), в една точка - т.О`. След като няма приплъзване, тази точка е обща за двата обекта. Като точка от равнината тя очевидно е неподвижна. Следователно ще бъде неподвижна и като точка от диска. Така, тази точка може да се разглежда като моментен център на скоростите. Скоростите на останалите точки ще се определят по формулите, показани на фигурата.

Трябва да се отбележи, че моментния център на скоростите е геометрична точка, и не бива да се отъждествява с материална точка от тялото. Така например, на снимката от фиг.8 моментния център е т.О`, но при по-нататъшното движение на колелото тази точка ще заеме мястото на т.А , а моментен център ще стане т.С и т.н.

Равнинното движението на диск, търкалящ се по равнина без приплъзване, трябва ясно да се разграничава от ротационното движение на диск, въртящ се около неподвижна ос &.

Класически случай на равнинно движение се среща при анализ на движението на коляно-мотовилков механизъм&.