РАЗРЕЗНИ УСИЛИЯ
|
|
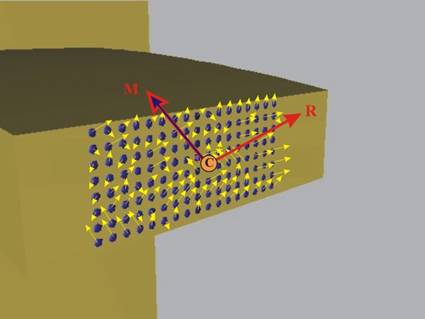
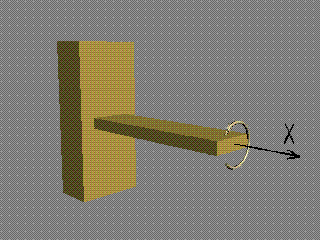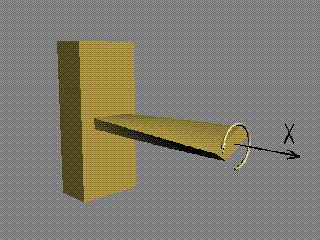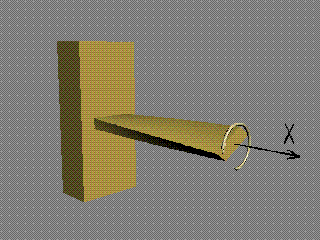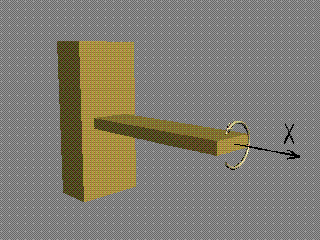
Нека да разгледаме конзолната греда от фиг.1. Прилагайки
метода на сечението и анализирайки междучастичните сили на взаимодействие
между лявата и дясната част, получаваме система
вътрешни сили, действащи върху лявото сечение (фиг.2). По принципа на действието и
противодействието, аналогична система действа и върху дясното сечение, но при
нея силите са с противоположни на първата система посоки.
Тези
сили са от особена важност в механиката на деформируемото тяло. Всеки
конструкционен материал има таван, до който могат да растат вътрешните сили,
без той да се разруши. Ако при дадено външно въздействие големината им достигне
тавана, характеризиращ материала на изделието, междучастичните връзки се
разкъсват, появяват се пукнатини и изделието се разрушава (счупва се на две,
обрушва се, разпада се на части и т.н.).
В тази и следващите теми ще си поставим
задача да изведем прости уравнения, с които да определяме тези сили.
Прякото
решаване на тази задача е сравнително сложно, поради големия (клонящ към
безкрайност) брой на частичките, а от там и на неизвестните сили. Като първа
стъпка при решаването на задачата ще намалим броя на неизвестните сили. Това ще
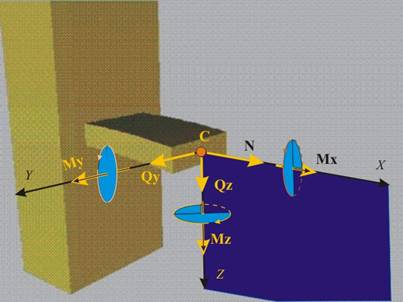
постигнем, като редуцираме системата сили спрямо центъра на тежестта на
сечението (фиг.3). Както е известно, такава пространствена система сили се
редуцира до динама, състояща се от главен вектор R
и главен момент М. Така
получаваме само две неизвестни обобщаващи (интегрални) характеристики на
вътрешните сили.
|
|
При аналитично решаване
на задачите използваме проекциите на двете интегрални характеристики върху една
дясно ориентирана правоъгълна координатна система. Това става така:
·
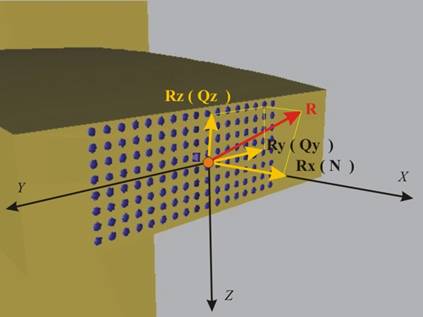
Първо, проектираме главния вектор върху оста, перпендикулярна на
сечението (в случая това е оста Х,
върху която получаваме проекцията Rx)
и върху самото сечение. Проекцията, която лежи в равнината на сечението,
разлагаме по осите Y (получаваме проекцията Ry) и Z (получаваме
проекцията Rz).
До
трите сили Rx, Ry и Rz стигнахме като
приложихме метода на сечението и разрязахме гредата на две части. Поради това
тези сили се наричат освен "вътрешни сили" още и "разрезни
сили". По-нататък двата термина ще се употребяват равностойно.
Силата
Rx е перпендикулярна (казва се още
"нормална") на сечението, поради което се нарича още "нормално
разрезно усилие" и се бележи с буквата N. Другите две сили са
допирателни (тангенти) към сечението, поради което се наричат "тангенциални
разрезни усилия" и се бележат съответно с Qy и Qz.
·
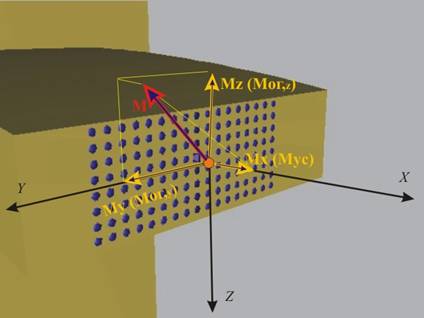
Второ, проектираме главния момент върху оста, перпендикулярна на
сечението (в случая това е оста Х,
върху която получаваме проекцията Мx) и върху самото
сечение. Проекцията, която лежи в равнината на сечението, разлагаме по осите Y (получаваме
проекцията Мy) и Z (получаваме
проекцията Мz).
Моментът
Мх върти в равнината на сечението и
"усуква" гредата. Поради това той се нарича още "усукващ
момент" и в някои учебници се отбелязва с Мус.
Моментите
Му и Мz въртят в равнини, перпендикулярни на
сечението и "огъват" гредата. Поради това те се наричат "огъващи
моменти" и в някои учебници могат да бъдат срещнати като Мог,у
и Мог,
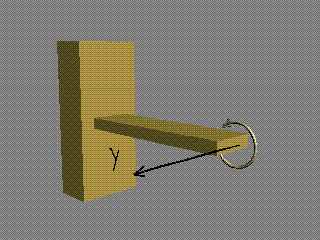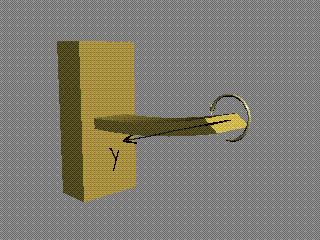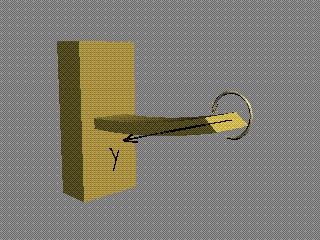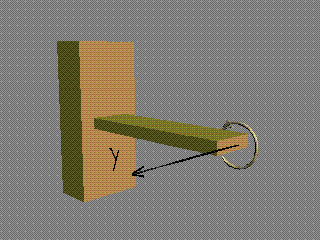

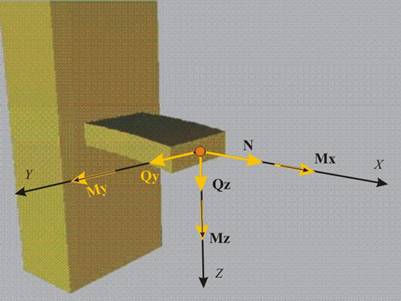
Така
можем да обобщим, че в общия пространствен случай вътрешните сили могат да
бъдат определени с шест разрезни усилия - три сили
(едно нормално разрезно усилие и две тангенциални разрезни усилия) и три
момента (един усукващ и два огъващи). Тези шест разрезни усилия се определят от
условието за локално равновесие на разглежданата част от гредата (в случая -
лявата). Както е известно, уравненията, които изразяват това
равновесие, също са шест, така
че задачата е статически определима.
|
Фиг. 9
Фиг. 10 |
В практиката често се
срещат случаи, при които натоварващите сили действат в една равнина. В този
случаи броят на разрезните усилия намалява. Нека да видим кои разрезни усилия
ще останат за равнината xCz (Фиг.7).
При силите ясно се
вижда, че тангенциалното разрезно усилие Qy е перпендикулярно на
равнината и няма да има проекция върху нея. Нормалното разрезно усилие и
тангенциалното разрезно усилие Qz лежат в равнината и се проектират с пълната си
големина.
При моментите трябва да
съобразим, че усукващият момент и моментът Mz въртят в равнини,
перпендикулярни на разглежданата и поради това няма да вземат участие в
решението. Само действието (въртенето) на огъващия момент Му е в равнина, успоредна на разглежданата.
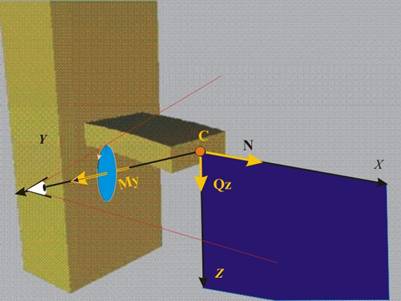
И така, когато
разглеждаме равнината хСz, в
решението ще участват само три разрезни усилия - нормалното разрезно усилие N, тангенциалното разрезно усилие Qz и
огъвъщият момент Му.
При такава равнинна
задача отпада необходимостта от
пространствено изобразяване на гредата и действащите сили. Изобразяването можем
да направим, като си представим, че равнината хСz съвпада с чертожният лист, а ние
наблюдаваме гредата срещу положителната посока на оста У (фиг.8).
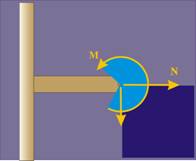
Това,
което бихме видяли при описаното положение, е изобразено на фиг.9. Разбира се,
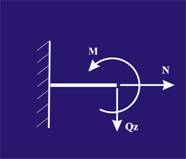
при решаване на задачите се представя схематизирано изображение, както на фиг.
10.

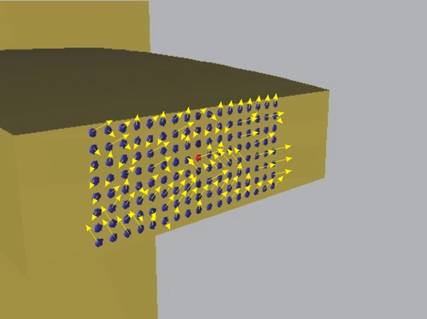 Фиг. 2
Фиг. 2