Условия за равновесие на произволна система сили.

Основните части (конструктивни елементи) на екипировката, с която се осъществява дадена технология или производствен процес, обикновено са неподвижни. Ако има подвижни части, то те са закрепени на неподвижни стойки или са поместени в неподвижни корпуси. За безаварийна работа е необходимо тези части да остават неподвижни, независимо от външните въздействия, породени от технологичния процес.

В една производствена среда или лаборатория, конструктивните елементи на машините и апаратите остават в покой, понеже се опират един на друг. Най-долните конструктивни елементи обикновено се опират на фундаменти, свързани със земната повърхност. Така всички механични въздействия, породени от технологичния процес и теглото на конструктивните елементи, се предават на земната основа.

Съществува голямо разнообразие за формата и размерите на отделните конструктивни елементи на машините и апаратите. В техническата механика те се схематизират до няколко основни форми - масивно тяло, плочи, черупки, греди, пръти и различни техни разновидности. Въпросите, свързани със схематизацията на формата на конструктивните елементи се дискутират в отделен модул, с който може да се запознаете, като щракнете тук. На изпита по тази тема те се смятат като допълнение и тяхното излагане не е задължително.

Взаимодействието на един конструктивен елемент с останалите елементи се осъществява в точките на закрепване. В тези точки прилагаме сили, с които моделираме това взаимодействие. Точките на закрепване на един конструктивен елемент могат да бъдат на произволно място по околната му повърхност. Поради това силите обикновено образуват пространствена (произволна) система. За да бъде конструктивния елемент в покой е необходимо системата сили, която действа върху него, да бъде уравновесена.

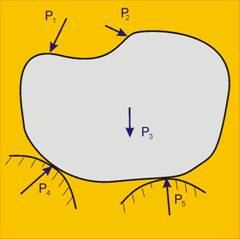
Фиг. 1

Нека да разгледаме тялото от фиг.1. То взаимодейства с други тела, за които служи като опора. Това взаимодействие е моделирано със силите Р₁ и Р₂ и в задачите се смята за известно (получено от предишни етапи на решението). Теглото на тялото Р₃ обикновено също се смята за известно, или ако е незначително, се пренебрегва.

За да остава в покой, разглежданото тяло се опира на други тела. В точките на опиране тялото ще въздейства върху опорите (акция). Обратното въздействие на опорите върху тялото (реакция) в нашия случай са силите Р₄ и Р₅. Такива сили се наричат опорни реакции.

И така, можем да обобщим, че конструктивните елементи в общия случай се намират под действието на произволна система външни сили, включваща сили на натоварване, собствено тегло и опорни реакции.

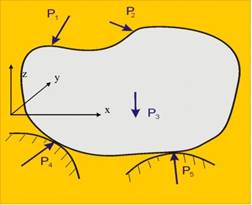
Фиг. 2

Уравненията, с които да анализираме равновесието на тази система сили, можем да получим от аналитичните условия за редукция. За да бъде една произволна система сили в равновесие, необходимо и достатъчно условие е динамата, към която системата се редуцира, да бъде равна на нула, т.е. да бъдат изпълнени едновременно условията R=0 и М=0

В общия случай (фиг.2) от векторното условие R=0 и М=0 се получават шест скаларни уравнения:

С тези шест уравнения могат да бъдат определяни шест опорни реакции (например Р4_х, Р4_у, Р4_z, Р5_х, Р5_у и Р5_z).

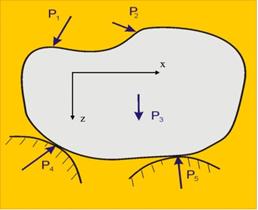
Фиг. 3

В равнинния случай (фиг. 3) от векторното условие R=0 и М=0 се получават три скаларни уравнения:

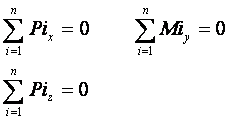
В равнинния случай със средствата на техническата механика се извеждат три уравнения за равновесие, с които могат да бъдат определяни три опорни реакции (например Р4_х, Р4_z и Р5, като в този случай направлението на Р5 трябва да е известно)

НАТАТЪК