Схематизация на опорните устройства.

Фиг.1 (·)

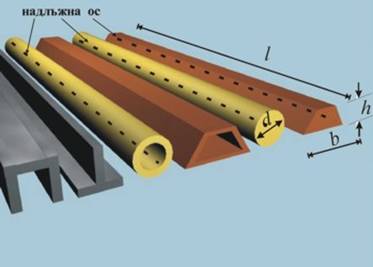
От всички възможни форми на конструктивните елементи, в техническата механика се разглеждат греди и пръти (фиг. 1) - тела, единият размер на които (дължината l) е много по-голям от другите два (ширината b и височината h).

Прътите са тела, които поемат сили само в двата си края. Силите задължително действат по оста на пръта (иначе няма да са в равновесие според първа аксиома) и го натоварват на опън (·) или на натиск (·).

Гредите са тела, които поемат сили без ограничения за направлението им по цялата си дължина. Такива сили ги натоварват на огъване (·).

Поради това, че два от размерите (ширина и височина) са много по-малки от дължината, при изобразяване на изчислителните схеми те често се пренебрегват, и гредите и прътите се изобразяват само с линии.

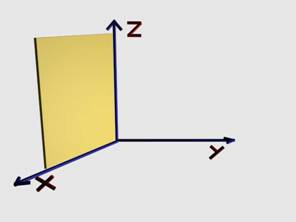
При решаване на задачи за анализ на равновесието на пространствена система сили се използва правоъгълна, дясноориентирана координатна система (фиг.2).

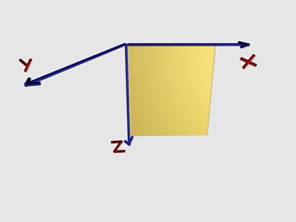
Изобразяването на гредата и опорите при решаване на равнинна задача се извършва в равнината Х0Z, като координатната система се ориентира така, както е показано на фиг.3.

Оста Х е хоризантална и насочена надясно.

Оста Z е вертикална и насочена надолу.

Посоките на двете оси определят и положителните посоки на силите.

·, ·

Фиг. 2 Фиг.3

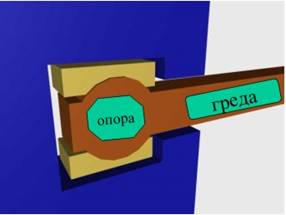
В реалните изделия опирането на конструктивните елементи рядко става через свободно лягане, както беше изобразявано до сега. По-често те се свързват със специално проектирани и изработени за целта опорни устройства. Тук ще се запознаем с три от тях, които ще използваме по-нататък в нашия анализ на равновесието на телата и при решаване на задачи от тази област.

Подвижна ставна опора (фиг.3)

Фиг. 3

Това е опорна устройство, което позволява в точката на опиране

гредата да се завърта (·)

и да се премества в дадено направление, например по оста х (наляво, ·).

Ограничава преместването в едно направление, например по оста z

(надолу, ·, и нагоре, ·).

В направлението, по което преместването е ограничено, се появява опорна реакция (в случая – вертикална, насочена на горе).

Схематично подвижната ставна опора се изобразява по следния начин:

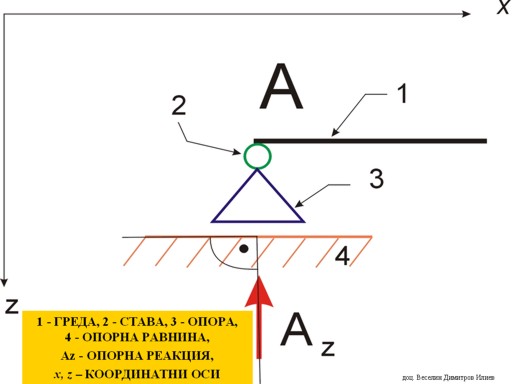
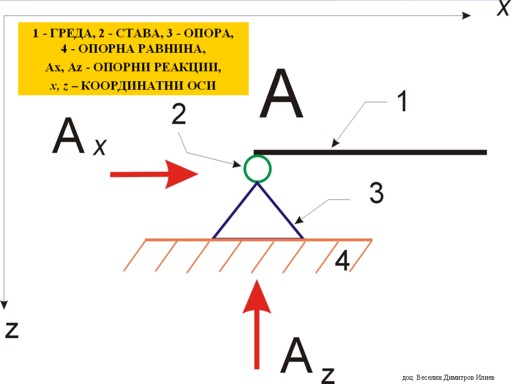
Неподвижна ставна опора (фиг. 4)

Фиг. 4

Това е опорно устройство, което позволява в точката на опиране

гредата да се завърта (·).

Ограничава преместването в две направления,

например по оста х (наляво, ·, надясно, ·),

и по оста z (надолу, ·, и нагоре, ·).

В двете направления, по което преместването е ограничено, се появяват опорни реакция (в случая – хоризонтална, насочена на дясно и вертикална, насочена на горе).

Схематично неподвижната ставна опора се изобразява по следния начин:

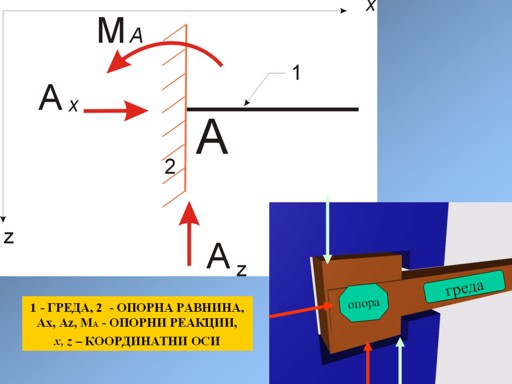
Запъване (фиг. 5)

Фиг. 5

Това е опорна устройство, което в точката на опиране

непозволява гредата да се завърта (·, ·),

и ограничава преместването в две направления,

например по оста х (наляво, ·, надясно, ·),

и по оста z (надолу, ·, и нагоре, ·).

В двете направления, по което преместването е ограничено, се появяват опорни реакция (в случая – хоризонтална, насочена на дясно и вертикална, насочена на горе).

При ограничаване на завъртането се появяват две сили с успоредни направления, еднакви големини и противоположни посоки – двоица сили.

Схематично запъването се изобразява по следния начин:

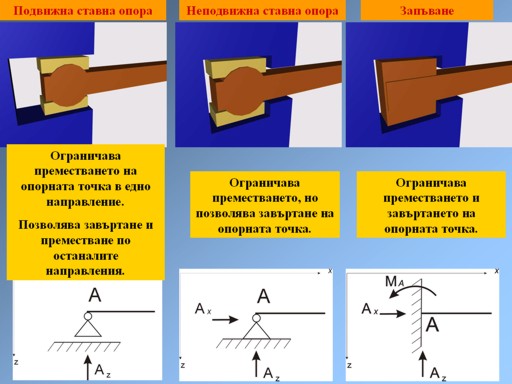
Ето едно обобщаване на трите вида опори:

В някои източници (учебници и ръководства за решаване на задачи) същите опорни устройства се изобразяват посредством пръти:

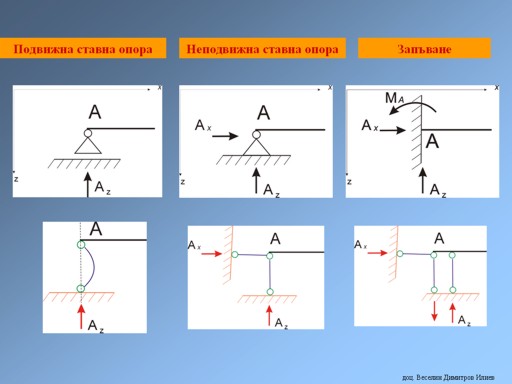
С изведените три независими уравнения за равновесие на равнинна система сили могат да бъдат определени три опорни реакции. От горната схема се вижда, че това ограничава вариантите на подпиране на гредата до три:

- запъване

- една подвижна и една неподвижна ставна опора

- три подвижни опори

Фиг. 6

Изведената система уравнения (две проекционни 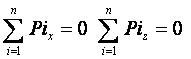и едно моментово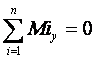) е

подходяща за приложение при запънатите греди. В този случай от всяко уравнение се получава по схемата от фиг. 6.

Фиг.7

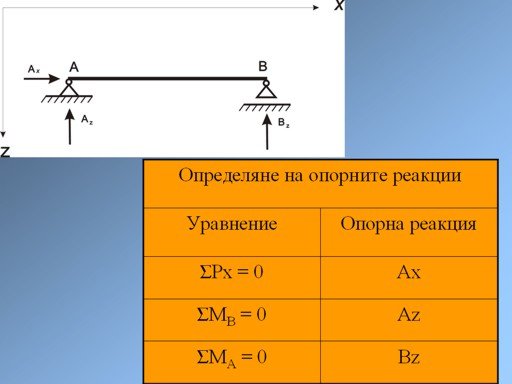
Ако същата система бъде приложена за греда на две опори, като тази на на фиг. 7, едно от проекционните уравнения ще има две неизвестни (в случая на фиг. 7 - по оста z - Az и Bz). Това създава определени трудности при решаване на задачата.

В този случай се препоръчва да се работи с едно проекционно и две моментови уравнения, по схемата на фиг. 7.

Фиг.8

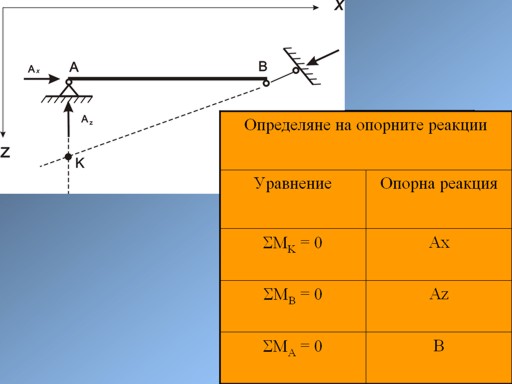
По същите причини, когато гредата е подпряна с три прътови опори, се препоръчва използването на три моментови уравнения по схемата на фиг. 8 (тук хоризонталната и вертикалната прътови опори в т.А са предствавени с една неподвижна ставна опора.

Приложението на трите препоръчителни схеми на решение има някои особености, свързани преди всичко с изискването използваните уравнения да са независими (да не са еквивалентни помежду си). Тези особености ще бъдат изяснени главно по време на аудиторните лекции и упражнения. Така че присъствайте редовно!

НАТАТЪК