ВЪВЕДЕНИЕ В
МЕХАНИКАТА НА ДЕФОРМИРУЕМОТО ТЯЛО
СИЛИ НА МЕЖДУЧАСТИЧНО ВЗАИМОДЕЙСТВИЕ.
МЕТОД НА СЕЧЕНИЕТО.
Както
вече беше казано, решението на задачата, която
сме си поставили тук, има пряко отношение към междучастичните връзки и формирането на
междучастичните сили. Тук този процес ще бъде илюстриран с анализ на
механичните процеси в конкретен обект.
|
Фиг. 6
Фиг.7 |
Нека да
разгледаме конзолната греда от фиг.1. Когато тя е свободна от външни
въздействия, междучастичните сили на привличане и отблъскване се уравновесяват.
Прилагането на външен товар предизвиква промяна на разстоянията между частиците
и увеличаване на вътрешните междучастични сили на привличане или отблъскване ·(фиг.2).
В
ежедневието, за да разберем структурата на един предмет, разделяме този предмет
на части (срязваме го или го счупваме), така, че да имаме поглед към неговата
вътрешност. По същия начин постъпваме и с гредата, като я срязваме с равнина,
перпендикулярна на остта й ·
(фиг.3). Отделяме дясната част и разглеждаме лявото сечение на гредата.
Стесняваме разглежданата област и увеличаваме мащаба (от макро-ниво минаваме на
микро-ниво) така, че да можем да виждаме частичките, които изграждат
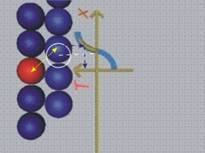
структурата на материала. Нека да изберем една частичка (червената) и да
направим анализ на силите, които действат върху нея (фиг.4).
При анализа ще направим предположението, че силите, с които частичката взаимодейства с останалите
частички, намаляват бързо с увеличаване на разтоянието, затова се взима предвид
само взаимодействието с преките съседи.
По
метода на суперпозицията пълната деформация
(която иначе е сложно явление) може да се разглежда като съвкупност от две
съставящи: деформация на отцепване и деформация на плъзгане.
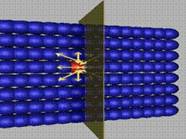
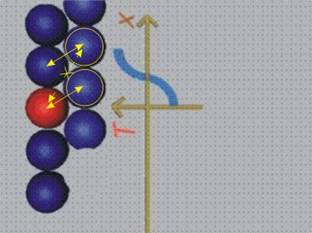
Деформация на отцепване имаме тогава, когато движението
на частиците, породено от външното въздействие,
е в направление, перпендикулярно (нормално) на разглежданата равнина · (фиг.5). Така частичките се сближават (междучастичното
разстояние намалява) или се раздалечават (междучастичното разстояние се
увеличава.
При премахване на външното въздействие, частичките
възстановяват първоначалната си конфигурация - деформацията на отцепване е
еластична.
Формирането
на междучастичните сили ще представим в координатна система xON. Оста х
е насочена по направление на преместването. Разглежданата точка се намира в
началото на координатната система, така че координатата х на съседната частичка
съвпада с междучастичното разстояние.
По оста
N ще
нанасяме големината на междучастичната сила. При промяна на междучадтичното
разстояние тази сила ще се описва с линията N=f(x). Равновесното състояние, което е показано на фиг.6 се
характеризира със стойност N=0.
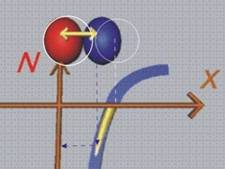
При
раздалечаване на частичките, се формира положителна сила на привличане. За всеки
материал тази сила има максимум, при достигане на който връзката между
частичките се разкъсва и започва процес на разрушаване ·
(фиг.7).
Такъв
процес на формиране на междучастичната сила се наблюдава при изделия, натоварени
на опън.
|
Фиг. 10c |
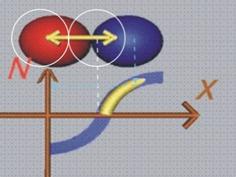
При
сближаване на частичките се формира отрицателна сила на отблъскване. Тук
функцията N=f(x) няма екстремум, така че междучастичната връзка
не се разкъсва ·
(фиг.8).
Такъв
процес на формиране на междучастичната сила се наблюдава при изделия,
натоварени на натиск.
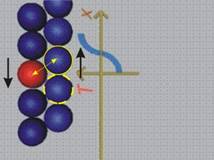
Деформация на плъзгане имаме тогава, когато движението на
частичките, породено от външното въздействие,
е в направление, успоредно (тангенциално) на разглежданата равнина (фиг.9).
При достигане на максималната стойност на междучастичната
сила · (фиг.10a), връзката между частиците се разкъсва (фиг.10b), но веднага се създава нова връзка с новата близка
съседна частица (фиг.10c). Разглежданата точка
попада в ново устойчиво равновесно положение, което тя запазва и след премахване на външното въздействие. Такава
деформацията се нарича пластична деформация.
|
|
Нека да
си поставим задача да определим пълната сила Р на междучастично
взаимодействие за разглежданата частичка с близка частичка от отстранената
дясна част на конзолата. Тя може да се получи по метода на суперпозицията, като
съберем силата N на отцепване и силата Т
на плъзгане (фиг.11).
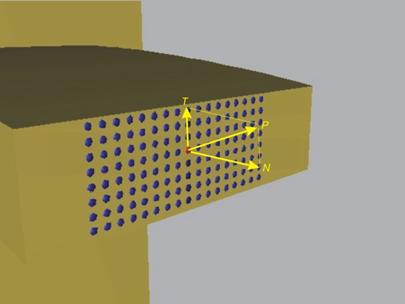
Ако приложим силите на междучастично
взаимодействие върху всяка точка от сечението, ще получим пространствена
система сили (фиг.12). По принципа на локалното равновесие, разглежданата лява част
на гредата трябва да се намира в равновесие под действие на външните сили и на
системата вътрешни силички, която компенсира липсата на дясната част.
И така, методът на сечението се състои в
разделянето на тялото с равнина и разглеждане на една от двете части, която
трябва да се намира в равновесие под действие на външните сили и вътрешните
силички, действащи в точките от сечението.
 Фит. 1
Фит. 1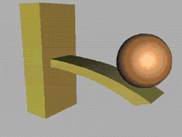
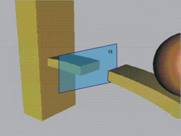 Фиг.3
Фиг.3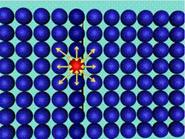
 Фиг.5
Фиг.5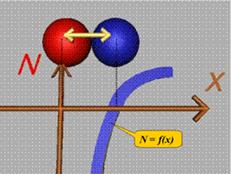
 Фиг.8
Фиг.8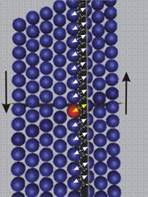
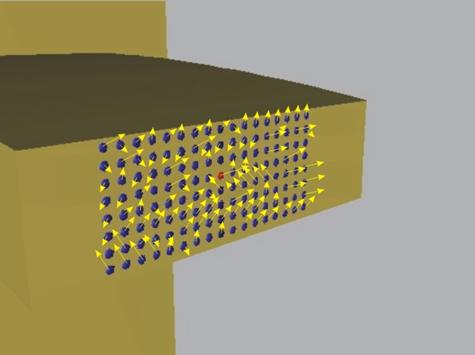 Фиг. 12
Фиг. 12