Редукция на произволна система сили спрямо дадена точка.

Фиг. 1

Фиг. 2 (·)

Когато разглеждаме твърдо тяло, силите, които действат варху него най-често са такива, че директрисите им не се пресичат в една точка. Така те образуват една произволна система сили, върху която правилата за редукция и условията за равновесие на сходяща система не могат да бъдат приложени. Когато силите действат в различни точки на тялото, правилото за събиране на сили е неприложимо . Това налага преди да бъде приложено правилото за събиране, силите да бъдат преместени с позволени операции в една предварително избрана точка. 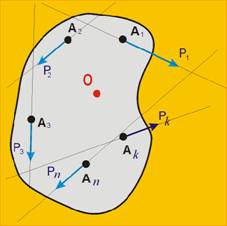Тази процедура ще бъде демонстрирана за случая, изобразен на фиг. 1.

Разглеждаме система от п на брой сили Р₁, Р₂ ... Р_к ...Р_п, приложени в точките А₁, А₂, ... А_к, ... А_п. Поставяме си задачата да ги съберем, като преди това ги пренесем в т.О. Нека да видим, как става това за силата Р_к.

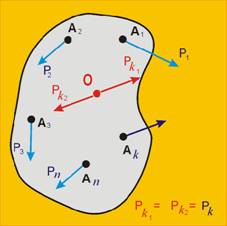
Първоначално в т.О се прилага уравновесена система от две сили Р_к1 и Р_к2, които са равни помежду си и на силата Р_к:

Р_к1 = Р_к2 = Р_к ,

имат обща директриса, противоположни посоки и направление, което е успоредно на силата Рк (фиг.2). Това е разрешена операция, според втора аксиома на статиката.

Фиг. 3 ( ·, ·)

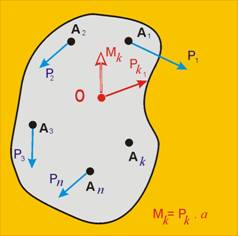
По построение системата от сили Р_к и Р_к2 представлява двоица сили, тъй като те са равни по големина, успоредни по направление и с противоположни посоки. Такива сили могат да бъдат заменени с момента на двоицата Мк (фиг. 3).

Като краен резултат от операцията остават силата Р_к1 и моментът Мк приложени в т.О.

По същия начин могат да бъдат преместени в т.О всички сили и да бъдат събрани - Р₁+Р₂+...Р_к+...Р_п=R. Силата R не е равнодействаща, тъй като освен нея в резултат на преместването се получава и момент. Тази сила се нарича главна сила или главен вектор на системата. Получените моменти (М₁ от преместването на силата Р₁, М₂ от преместването на силата Р₂ и т.н.) също събираме по правилото за събиране на вектори - М₁+М₂+...+М_к+...М_п=М. Полученият момент се нарича главен момент на системата.

И така, можем да обобщим, че една произволна система сили се редуцира спрямо дадена точка до главна сила R и главен момент M, които съвкупно се наричат "динама". Процедурата е илюстрирана на фиг. 4.

Фиг.4

Описаният начин за редукция е по-скоро графичен. Необходимите уравнения за аналитична редукция можем да получим по познатия от сходяща система начин, като проектираме силите и моментите върху осите на една правоъгълна координатна система Oxyz.

P_1x, P_1y, P_1z - компоненти на силата P₁ ; M_1x, M_1y, M_1z - компоненти на момента M₁

P_2x, P_2y, P_2z - компоненти на силата P₂ ; M_2x, M_2y, M_2z - компоненти на момента M₂

.

.

P_kx, P_ky, P_kz - компоненти на силата P_k ; M_kx, M_ky, M_kz - компоненти на момента M_k

.

.

P_nx, P_ny, P_nz - компоненти на силата P_n ; M_nx, M_ny, M_nz - компоненти на момента M_n

Главната сила ще има три компоненти. Същото важи и за главния момент.

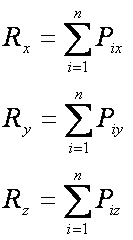
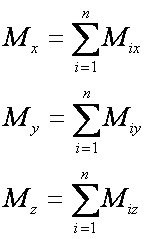
три проекционни уравнения три моментови уравнения

Пълните големини, направленията и посоките на двата елемента от динамата се получават по същия начин, както при равнодействащата на сходяща система сили.

Ако срещате тези математични изрази за първи път, сега те може да Ви изглеждат чужди. Но ако посещавате редовно аудиторните занятия и самостоятелно работите варху задачите, които се решават с тези формули, ще видите, че те всъщност са много лесни за приложение. Тук може да намерите решението на един такъв пример. За целта ще ви е необходима програмата Acrobat Reader, инсталация за която можете да изтеглите тук.

НАТАТЪК