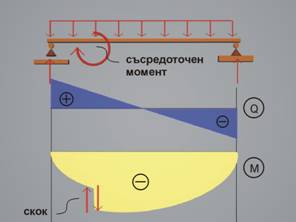
ТЪЛКУВАНЕ НА ДИФЕРЕНЦИАЛНИТЕ ЗАВИСИМОСТИ

ПРАКТИЧЕСКИ ПРАВИЛА ЗА ОПРЕДЕЛЯНЕ НА РАЗРЕЗНИТЕ УСИЛИЯ

1. Правило на скоковете

При математическия анализ на разрезните усилия, те се представиха като функции на координатата х: N(x) - за нормалното разрезно усилие, Q(x) - за тангенциалното разрезно усилие и М(х) - за огъващия момент. При извода на уравненията за определяне на тези функции и диференциалните зависимости между тях беше споменато, че изведените изрази важат само в отделни участъци. Най-често тези участъци са разделени от приложени съсредоточени сили и моменти. От математична гледна точка те прекъсват и начупват функциите, което на диаграмите се изразява със скокове и чупки. Тук ще бъдат разгледани само най-често срещаните случай.

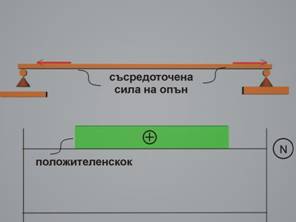
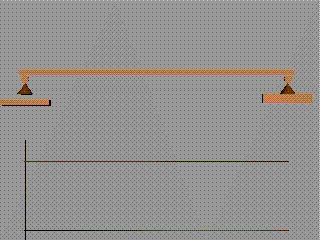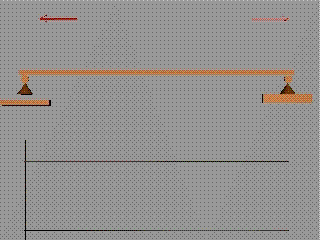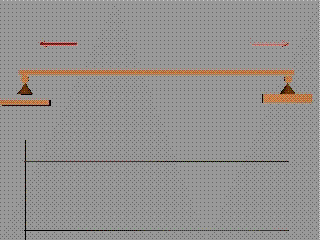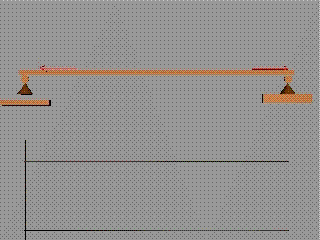
- За нормалните разрезни усилия

Където в схемата на натоварването има приложена съсредоточена хоризантална сила, диаграмата на нормалните разрезни усилия прави скок, равен на големината на силата.

Ако силите натоварват даден участък от гредата на опън,

нормалното разрезно усилие е положително.

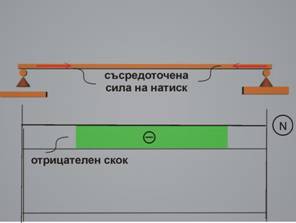
Ако силите натоварват даден участък от гредата на натиск,

нормалното разрезно усилие е отрицателно.

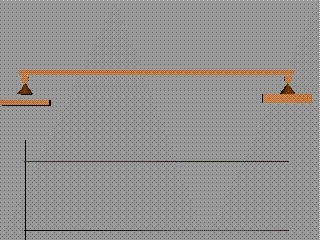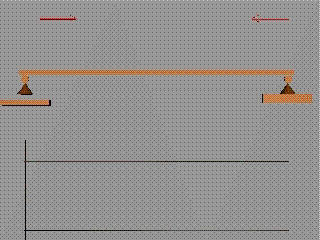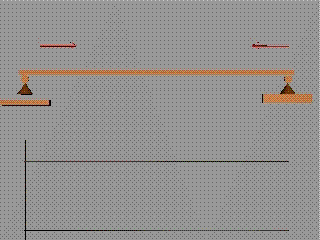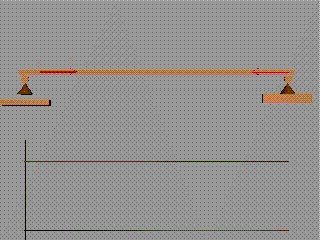
- За тангенциалните разрезни усилия

Където в схемата на натоварването има приложена съсредоточена вертикална сила, диаграмата на тангенциалните разрезни усилия прави скок.

Големината на скока е равна на големината на силата.

Посоката на скока съвпада с посоката на силата.

Допълнение: Съсредоточената сила предизвиква чупка в диаграмата на огъващия момент

- За огъващия момент

Където в схемата на натоварването има приложен съсредоточен момент, диаграмата на огъващия момент прави скок, равен по големина на големината на момента.

За определяне на посоката на скока има много правила.

Едно от тях се гради на представата, че двоицата, която поражда съсредоточения момент, действа върху диаграмата като ножица.

На фигурата е показан скок, породен от двоица с отрицателен момент.

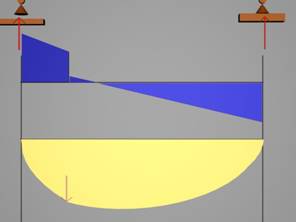
2. Правила на площите

Нека да разгледаме участък от гредата, в който има приложен разпределен товар с интензивност q_(х). Между тангенциалното разрезно усилие и разпределения товар беше изведена диференциалната зависимост

,

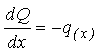която може да бъде представена още като . Тази зависимост може да бъде интегрирана в границите на участъка по следния начин:

- За лявата страна на равенството dQ → .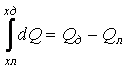

В този израз хл означава стойността на координатата х в лявата граница на участъка (за интеграла се явява долна граница), хд - стойността на координатата х в дясната граница (за интеграла се явява горна граница), Q_д и Q_л са стойностите на тангенциалното разрезно усилие съоотведно в дясната и лявата граница на участъка.

- За дясната страна на равенството → .

От математиката е известно, че определеният интеграл дава плащта, ограничена между оста х и функцията q_(х) в рамките на участъка. Тази площ ще означим с Fq.

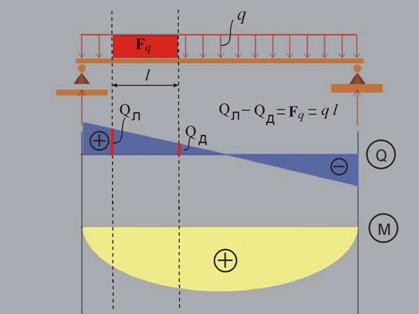
Като съберем резултатите за двете страни на равенството се получава Q_д - Q_л = - Fq, а като умножим двете страни с (-1)

Q_л - Q_д = Fq

От този израз може да бъде дефинирано първото правило на площите, свързващо стойностите на

Q-диаграмата и площта на разпределения товар.

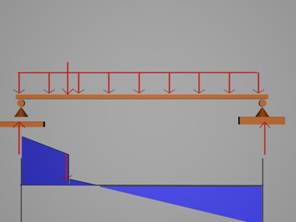
За даден участък от гредата, разликата между стойностите на тангенциалното усилие в лявата и дясната граница е равна на площта на фигурата, изобразяваща разпределения товар.

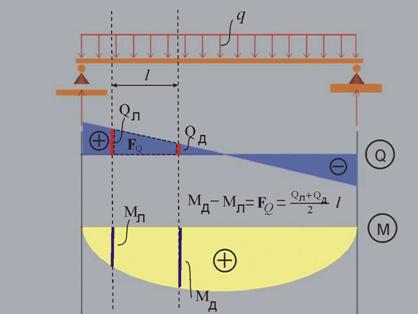
Аналогично правило може да бъде изведено за стойностите на М-диаграмата и площта на Q-диаграмата след интегриране на диференциалната зависимост между двете функции:

→ →

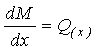M_д - M_л = - F_Q

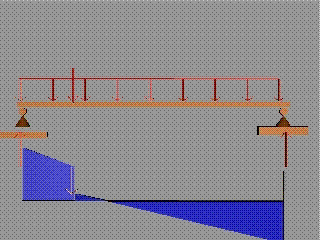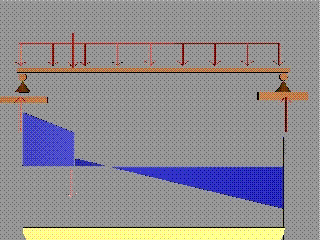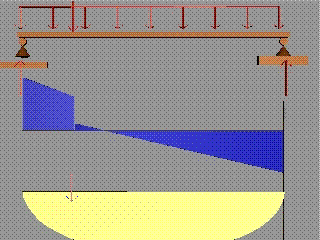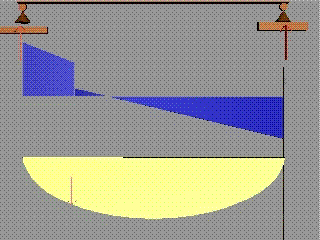
За даден участък от гредата, разликата между стойностите на огъвъщия момент в дясната и лявата граница е равна на площта на фигурата, изобразяваща тангенциалното разрезно усилие.