Н А П Р Е Ж Е Н И Е

Разрезните усилия дават обща представа за големината на силите на междучастично взаимодействие в дадено сечение, но не дават отговор на въпроса за стойностите на тези сили в отделните точки. Точно тези стойности стават причина за разрушаване на телата и тяхното познаване е от първостепенна важност в механиката на деформируемото тяло. Основното затруднение при извода на формулите за тяхното определяне е големият им брой, клонящ към безкрайност. Това затруднение се избягва с въвеждане на понятието "напрежение".

Фиг.1

Фиг.2

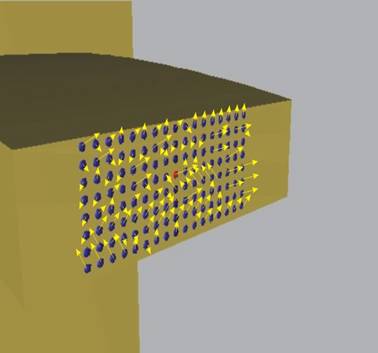
При анализиране на механичното поведение на дадено тяло и прилагайки метода на сечението, достигаме до съвкупност от частици и сили на взаимодействие, действащи върху тях (фиг.1).

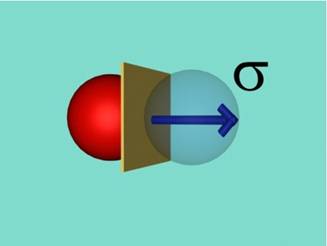
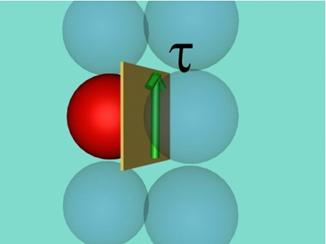
Сега на всяка частичка ще присъединим област от напречното сечение с площ A=d² (d - диаметър на частичката). По-нататък тази област ще наричаме "площадка". Такъв модел по-добре изпълнява хипотезата за непрекъснатост на материала (фиг.2).

Напрежението представлява стойността на силите на междучастично взаимодействие за единица площ.

Фиг.3

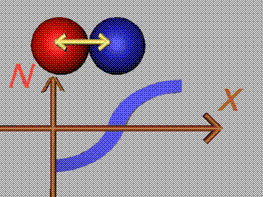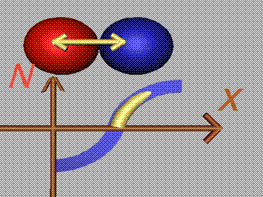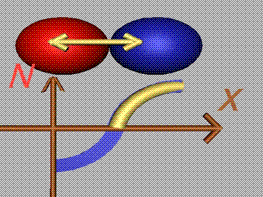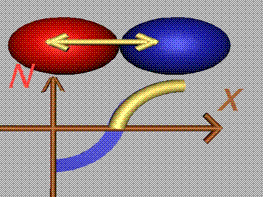
При отцепване на на слоевете, между частичките се формира нормална сила N. Тази сила разпределяме върху площта, присъединена на частичката (площта на площадката), и получаваме нормалната компонента на напрежението (фиг.3).

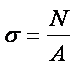(1)

Формално, връзката между силите и напреженията може да се разглежда както връзката между натиска и налягането. Така, както натискът, разпределен върху площта, дава налягане, така силата, разпределена върху площта, дава напрежение.

Фиг.4

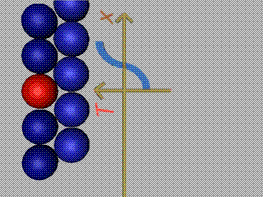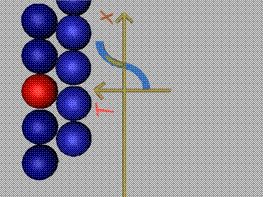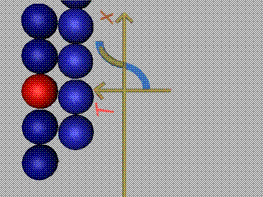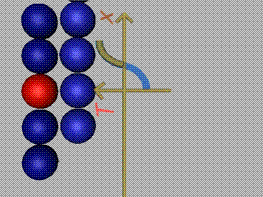
При хлъзгане на слоевете, между частичките се формира тангенциална сила Т. Тази сила разпределяме върху площта, присъединена на една частичка (площта на площадката), и получаваме тангенциалната компонента на напрежението (фиг.4).

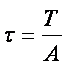(2)

Фиг.5

Фиг.6

- За една и съща частичка може да бъде разгледано отцепването или плъзгането на различни слоеве, в които тя участва.

- Различните слоеве имат различно направление.

- В различните слоеве тя ще има различни съседни частички, с различно междучастично радстояние, което значи, че и площадките ще бъдат различни.

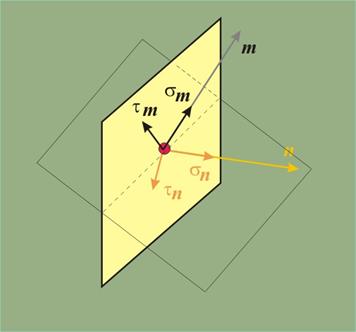
- Площадките за една точка но в слоеве с различно направление ще бъдат определяни с техните нормали n.

- Компонентите на напрежението ще носят индекс, който да показва площадката, за която са получени

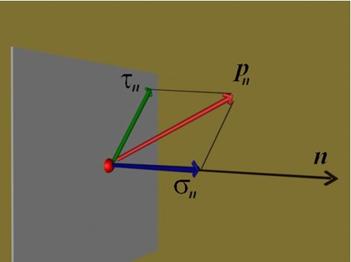
s_n и t_n за площадка с нормала n, s_m и t_m за площадка с нормала m и т.н. (фиг.5).

Двете компоненти на напрежението може да бъдат събрани и да бъде получено пълното напрежение р (фиг.6).

В следващите теми ще бъде показано, как уравнения (1) и (2) могат да бъдат използвани за определяне на напреженията в конкретни случаи. При това за по-кратко изложение нормалната компонента ще бъде наричана "нормално напрежение", а тангенциалната - "тангенциално напрежение".