Деформация

В предишна тема беше въведен модел на материала, от който са изградени телата, като съставен от частици с безкрайно-малки размери (материални точки). При външно въздействие телата променят формата и размерите си. При това разстоянията между частиците се променя – те се преместват, като в различните части на тялото големината на тези премествания е различна. За да се характеризира интензивността на нарастване или на намаляване на преместванията се въвежда понятието “деформация” като мярка за промяната на формата и размерите на телата.

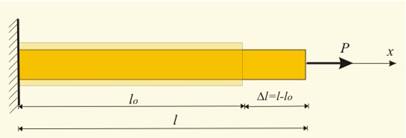
Фиг.1

Едно външно въздействие (сила Р), приложено само по една ос (например по оста х, фиг.1), предизвиква промяна на линейните размери ·. Ако началният размер на тялото по тази ос е l₀, а размерът след деформиране - l, разликата

,

се нарича “абсолютна надлъжна линейна деформация”.

За понятията: “надлъжна”, а не “напречна”; “линейна”, а не “ъглова”.

При формирането на абсолютната деформация, освен външното въздействие и вида на материала, роля играе и размерът на тялото. Колкото е по голямо тялото, толкова по-вече материал има “за деформиране” и толкова по-голяма деформация се формира. Това пречи да се сравнява механичното поведение на тела с различни размери. За да се елиминира влиянието на размерите, се въвежда понятието “относителна линейна деформация e” :

.

Деформацията е положителна при удължение () и отрицателна при скъсяване ().

Линейната деформация се формира от нормалното напрежение. В Техническата механика се приема линейна връзка между нормалното напрежение s и линейната деформация e ·:

.

Този израз се нарича “закон на Хук”, а коефициентът на пропорционалност Е – модул на еластичност.

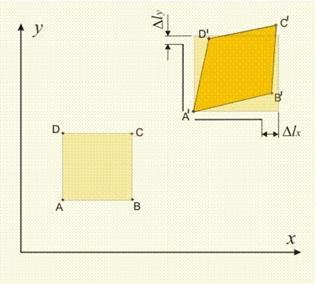
Фиг.2

Промяната на надлъжните размери (по направление на оста х), предизвиква промяна и на напречните размери · (в направления перпендикулярни на оста х). Например на примера от фиг.2, напречният размер а₀ се променя в а след деформацията. Абсолютната деформация е

,

а относителната деформация се означава като :

.

От фиг.2 се вижда, че когато надлъжната деформация е положителна (удължение по х), напречната е отрицателна (скъсяване в направление, перпендикулярно на х). Освен това е установено, че може да бъде приета линейна връзка между напречната и надлъжната деформация:

.

Коефициентът на пропорционалност m се нарича “коефициент на Поасон”.

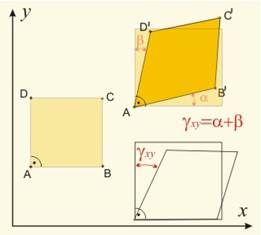
Фиг.3

Когато външното въздействие е равнинно ·, и по двете оси в равнината се формира надлъжна деформация, което налага в означението на деформациите да се въведе долен индекс. Например за схемата на фиг.3 се получава ·

:

за деформацията по оста х,

за деформацията по оста у.

Фиг.4

Промяната на формата на телата се характеризира с ъгловата деформация , която се дефинира като промяна на правите ъгли на тялото. Например на фиг. 4 в начално, недеформирано състояние, ъгълът ВАD е прав. При деформиране на тялото отсечките АВ и AD се завъртат до AB’ и AD’ (ъглово преместване) и ъгълът В’АD’ вече не прав. Разликата

е ъгловата деформация в равнината хОу ·.

Ъгловата деформация се формира от тангенциалното напрежение. В Техническата механика се приема линейна връзка между тангенциалното напрежение t и ъгловата деформация g · по закона на Хук за ъгловите деформации:

,

където G е модул на ъгловите деформации.

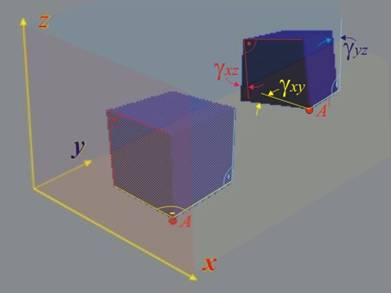
Фиг.5

Аналогично за другите координатни равнини при тримерна деформация се получават g_хz и g_уz · (фиг.5).