СФЕРИЧНО И ОБЩО ДВИЖЕНИЕ НА ТЯЛО.

Фиг.1 ·

Фиг.2 ·

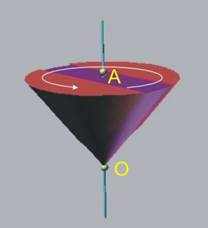
В предишна тема разгледахме движението на тяло, което има две неподвижни точки О и А (фиг.1). Тези точки определят една ос на ротация, а движението си нарича "Ротационно"Ã.

Нека сега да предположим, че за същото тяло неподвижна остава само т.О. Възможно е тялото да продължи да се върти около оста на ротация, на тя вече няма да бъде неподвижна. Единственото нещо, което може да се каже за нея е, че тя винаги ще минава през т.О.

Фиг. 3

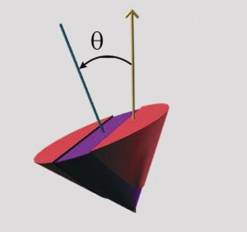
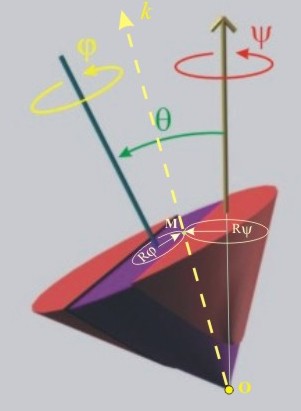
Тъй като тялото е недеформируемо, движението на всяка точка от него ще се подчинява на условието разстоянието между нея и неподвижната точка да е постоянно. Така например, т.М от фиг.3 по време на движението си, в различни моменти ще заема различни положения, но всички те ще отстоят на еднакво разстояние R от неподвижната т.О. Геометричното място на точките, намиращи се на идно и също разстояние от една точка, е сферата. Поради това, движението на тяло с една неподвижна точка, се нарича "сферично".

Сферичното движение на тяло може да бъде определено със закона, по който то се върти около някаква ос (ос на собственото въртене) и закона по който тази ос се движи в пространството.

Фиг.4 ·

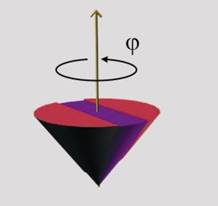
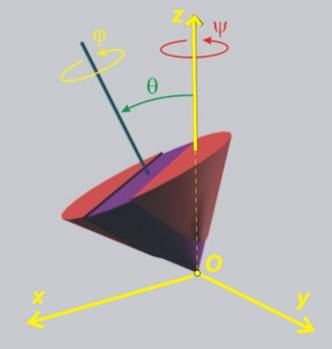
Както е известно от предишните теми, въртенето на тялото около неподвижна ос се описва с ъгъла на собствено въртене j (фиг.4).

Фиг.5 ·

Движението на оста на собствено въртене в пространството се определя от два ъгъла.

Ъгълът q, на който оста на собствено въртене се отклонява от кординатната ос по време на движението, се нарича ъгъл на нутация (фиг.5).

Фиг.6 ·

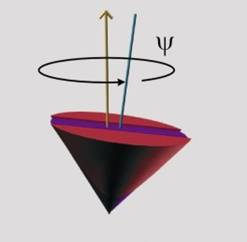
Ъгълът y, на който оста на собствено въртене се завърта около кординатната ос по време на движението, се нарича ъгъл на прецесия (фиг.6).

Фиг.7

Познаването на тези три ъгъла определя положението на тялото спрямо неподвижната координатна система Оxyz (фиг.7). Следователно, сферичното движение на тяло има три степени на свобода.

Трите зависимости на тези ъгли от времето t ще представляват закона на движение. Следователно, законът на движението на тяло около една неподвижна точка ще се изразява с три уравнения:

j = f₁(t)

q = f₂(t)

y = f₃(t)

Фиг.8

Фиг. 9

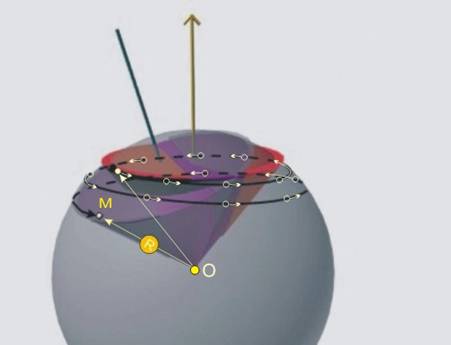
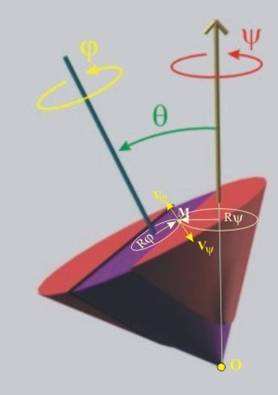
Скоростта, с която една т.М от тялото се завърта около оста на собствено въртене, може да бъде определена по формулата

.

където wj е ъгловата скорост, а Rj е разстоянието от точката до оста (фиг.8).

Скоростта, с която същата точка се завърта около координатната ос, може да бъде определена по формулата

.

където wy e ъгловата скорост, а Ry е разстоянието от точката до оста (фиг.8).

Както се вижда от фигурата, двете скорости имат едно направление но противоположни посоки.

Винаги можем да намерим такава т.М, която да отстои от двете оси на разстояния, за които да е изпълнено отношението

,

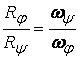така че ,

или Vj = Vy.

Тъй като двете скорости имат противоположни посоки, за скоростта на т.М ще получим:

V_M = Vj + Vy = 0,

или т.М ще бъде неподвижна.

Двете точки М и О определят права k, точките на която са неподвижни в разглеждания момент. Както при равнинното движение беше дефинирана неподвижна точка като моментен център на скоростите, така и при сферичното движение правата k може да бъде дефинирана като моментна ос на въртене (ос на ротация). В различните моменти тя има различни направления, които обаче винаги минават през т.О. Така сферичното движение може да бъде разглеждано като поредица от последователни завъртания около моментните оси на ротация.

Информацията в направеното до тук изложение е достатъчна, за да получите на изпита пълния актив за този въпрос. Трябва да знаете обаче, че това представяне на сферичното движение е твърде опростено. За пълноценно боравене с тази материя е необходимо по-задълбоченото й изучаване от съответните литературни източници.

ОБЩО ДВИЖЕНИЕ НА ТЯЛО

Фиг.10

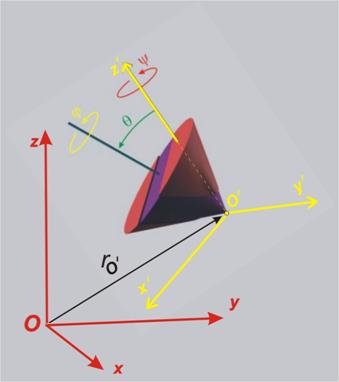
Един от подходите при дефиниране на общото движение е да се изходи от сферичното. Както се видя от изложението по предишната тема, единственото ограничение, което се налага върху тялото при сферичното движение, е една точка от тялото да бъде неподвижна. Ако отпадне и това ограничение, движението може да се нарече "общо", без никакви ограничения.

За да опишем движението на тялото при този подход, към трите уравнения на сферичното движение Ã трябва да прибавим и три уравнения (при координатен метод Ã) от закона на движение на точката (т.О' на фиг.10). Следователно, общото движение има шест степени на свобода, а законът на движение има вида:

j = f₁(t),

q = f₂(t),

y = f₃(t).

X_О' = x(t) ,

Y_О' = y(t) ,

Z_О' = z(t) .

Един друг подход, който е необходимо да изложите на изпита, ако Ви се падне този въпрос от конспекта, беше описан в началото на раздела Ã.