КИНЕМАТИКА НА СЪСТАВНО ДВИЖЕНИЕ НА ТОЧКА.

В предишни теми разгледахме случаи на определяне на скорости и ускорения на точки от тела, извършващи ротационно или равнинно движение. Съществуват обаче случаи, когато една точка участва едновременно в две или по-вече движения. Такова движение на точка се нарича "съставно".

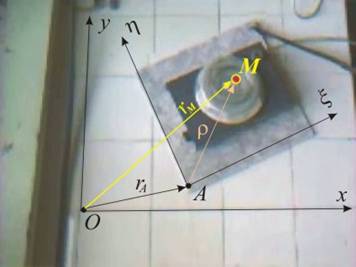
Нека да разгледаме работния елемент на една електромагнитна бъркалка. Когато тя е поставена неподвижно върху работния плот, точките от работния елемент могат да бъдат разгледани като точки от тяло, извършващо ротационно движение·. Нещата се усложняват, ако задвижим бъркалката спрямо работния плот. Тогава работният елемент се премества спрямо съда и основата на бъркалката, но едновременно с това той, заедно с всички части на бъркалката участва в движението спрямо плота·.

Фиг.1

Фиг.2

За описание на движението на бъркалката в този случай можем да използваме неподвижната (абсолютната) координатна система Оху, свързана с неподвижния плот, и подвижната (локална) координатна система Оxh, свързана с движещата се основа на бъркалката (фиг.1).

Положението на една движеща се точка М · можем да определим както спрямо неподвижната координатна система с радиус-векторa r_M (фиг.2), така и спрямо подвижната координатна система с радиус-векторa r. Трябва да се отбележи, че за разлика от точките на тяло, извършващо равнинно движение, тук радиус-векторът r е променлив както по направление, така и по големина (дължина)·.

Движението на т.М спрямо неподвижната координатна система ще бъде напълно определено, ако се познава законът на движение

.

От фиг.2 се вижда, че радиус-векторът на т.М може да се представи с векторната сума

.

Приблизително можем да кажем, че r описва движението на точката в рамките на подвижната координатна система, а r_A - на подвижната координатна система (без завъртането) спрямо неподвижната. В техниката често се срещат случаи, при които движението на точката спрямо неподвижната координатна система е много сложно, но разгледани по отделно, движението на точката спрямо подвижната система и движението на подвижната система спрямо неподвижната са прости. За удобство са въведени три понятия за трите вида движения:

r Абсолютно движение - движението на т.М спрямо неподвижната (глобалната) координатна система.

r Относително (релативно) движение - движението на т.М спрямо подвижната (локалната) координатна система.

r Преносно движение.

Това движение изисква по-подробно пояснение. Нека си представим т.М като неподвижна спрямо локалната координатна система ("замръзнала" в системата Оxh). Тогава тя ще се движи заедно с всички точки от тази система. Движението на т.М спрямо неподвижната координатна система като "замръзнала" в локалната система, се нарича преносно движение.

Трите движения и формирането на скоростта и ускорението на т.М при съставно движение ще бъде илюстрирано със следния пример:

Фиг.3 ·

Фиг.4

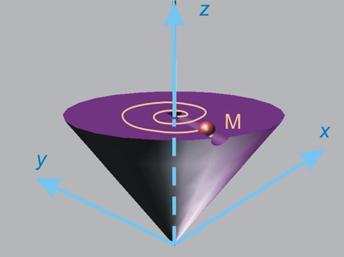
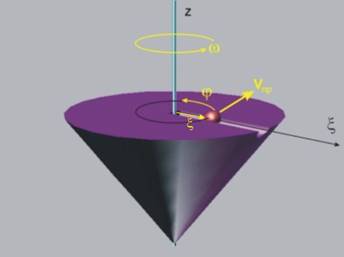
Нека да разгледаме едно тяло, което се движи ротационно спрямо неподвижната координатна система и т.М, която се движи праволинейно спрямо тялото ·.

Ротационното и праволинейното движение не са от най-сложните за анализ движения. Движението на точката спрямо неподвижната система обаче, ще бъде далеч по-сложно от праволинейното (фиг.3).

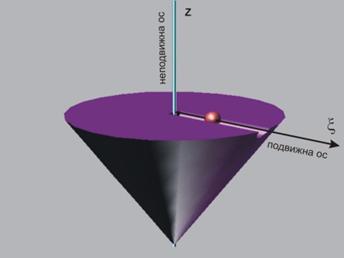
За неговото изучаване може да бъде фиксирана една неподвижна ос на въртене z, за описание на ротационното движение на тялото и една подвижна ос x за изучаване на праволинейното движение на точката спрямо тялото (фиг.4). Нека да разгледаме тези движения:

Фиг.5 ·

r Относително движение - праволинейното движение на точката спрямо оста x (тялото не се движи, фиг.5).

Законът на движение ще бъде x=x(t).

Скоростта на точката при това движение се нарича "относителна скорост" и ще бъде

.

Фиг.6 ·

r Преносно движение - въртенето на точката заедно с тялото около оста z (фиг.6).

Законът на движение ще бъде j=j(t), а скоростта на въртене - .

Скоростта на точката при това движение се нарича "преносна скорост" и големината й ще бъде (скорост на точка от тяло, извършващо ротационно движение):

.

Фиг.7

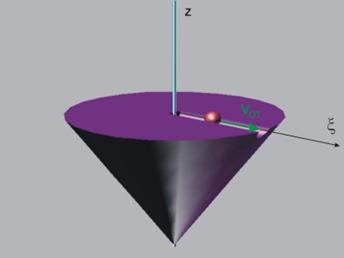
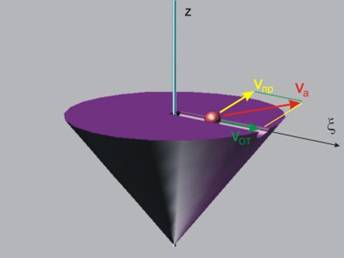
r Абсолютно движение - движението на точката спрямо неподвижната координатна система

Скоростта на точката при абсолютното движение се нарича "абсолютна скорост" Va и се определя като сума от относителната и преносната скорост. Скоростите са векторни величини и сумирането трябва да бъде извършено по правилата за сумиране на вектори (фиг.7).

Va = Vот + Vпр.

При получаване на абсолютното ускорение се подхожда по същия начин. Тук обаче математичният извод е твърде сложен поради факта, че радиус-векторът на относителното движение е променлив както по направление, така и по дължина ·, което твърде усложнява неговото диференциране. На този етап е достатъчно да знаете, че в някои случаи, дори преносното и относителното движения да са равномерни, когато преносното движение е ротационно, съществува едно допълнително, кориолисово ускорение. Така че в общия случай, абсолютното ускорение aa се получава като векторна сума от относителното ускорение aот, преносното ускорение aпр и кориолисовото ускорение aкор:

aa = aот + aпр + aкор.

Нещо по-вече за кориолисовото ускорение може да научите тук ® &.