Кинематика на точка. Закон на движението. Траектория.

Забележка: В това изложение знакът Ã , поставен в текста до термин, който Ви се вижда непознат, позволява да се върнете и да си припомните обяснение от вече четен текст через връзка, която се активира със щракване върху този знак.

Знакът & пък ще Ви отведе до място, където можете да получите допълнителна информация или да проследите конкретно решение на разглеждания проблем.

С тази тема започва нов раздел от дисциплината "Техническа механика" - "Кинематика" Ã, в който ще анализираме кинематичното състояние на обектите Ã. Анализа ще започнем с разглеждане на най-простия обект - материална частица (материална точка), но преди това ще бъдат въведени някои понятия, необходими за разбиране на по-нататъшното изложение.

- Кинематиката е дял от механиката, в който се изучава движението на телата, без да се отчитат причините, породили това движение (както ще видим по-нататък, това обикновено са някакви сили).

- Обект на механиката е механичното движение - изменението на взаимното положение на телата, извършващо се в пространството и времето·. При това едно от телата се избира за неподвижно и към него се свързва координатна система. Ако използвате електронния вариант на лекциите, за Вас това ще бъде екрана на монитора. Така, по-нататъшното описание на движението става спрямо тази координатна система· (спрямо екрана).

- До сега и друг път се е налагало да използвам движението на телата при описание на някои обекти - работа на опорните устройстваÃ, получаване на ротационна повърхнинаÃ, момент на сила спрямо точкаÃ, двоица силиà и др. В тези случаи обаче, времето, за които се извършва движението не беше от значение. В Кинематиката се работи с понятия като скорост и ускорение, така че времето е от първостепено значение. Използва се астрономическото време, което се изменя от миналото към бъдещето и се измерва в секунди, а в математичните изрази се въвежда като скаларна, непрекъснато изменяща се независима величина.

- Основно при анализа ще бъде използвана правоъгълна координатна система. Освен нея ще бъдат използвани и други начини за определяне положението на точката - векторен , при който се получават най-общите, универсални уравнения за описание на движението, и естествен, удобен в някои частни случай на движение. За всяка от координатните системи характеристиките на движението ще бъдат разгледани по отделно. Не е необходимо да се притеснявате, ако не сте запознат с особеностите на тези системи, тъй като всичко необходимо за настоящия анализ ще бъде дадено тук.

r Векторен метод

Фиг.1

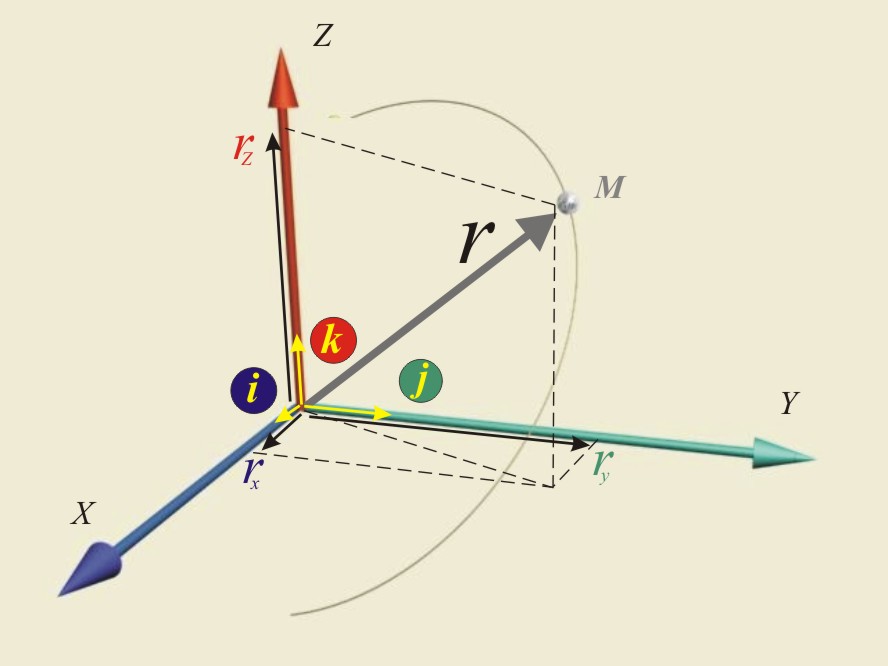
При векторният метод положението на точката М се определя от вектор r с начало в неподвижната т.О и край в т.М (радиус-вектор, фиг.1). Така, за да познаваме положението на една точка М, ако тя е неподвижна, е необходимо да знаем четири числа (координати) - дължината на радиус-вектора и трите ъгъла a, b, g, които той сключва с координатните оси. Обикновено, за да се избегне влиянието на мерките за ъглите (радиани, градуси, гради), вместо ъглите се дават техните косинуси (посочни косинуси на вектора). Само два от трите посочни косинуса са независими (ако знаем два от тях, можем да изчислим третия), така че положенито на т.М се определя с три координати.

Очевидно, ако т.М се движи, координатите й се изменят с течение на времето· т.е. радиус-векторът става функция на времето (t). За да познаваме движението на точката, трябва да знаем нейното положение (трите координати) във всеки момент от времето. Това положение се дава от три уравнения, свързващи координатите на точката с времето, които могат да се обобщят като r=r(t). Тези уравнения представляват закона на движението на точката.

Когато по някакъв повод стане дума за закон на движението в механиката, не е необходимо да се мъчите да си спомните някаква текстова формулировка. Необходимо е да си спомните уравненията.

Фиг.2 ·

При движението си материалната точка съвпада с различни геометрични точки·. Съвкупността от геометричните точки в пространството, с които съвпада в различните моменти от движението си т.М, се нарича траектория на т.М. Траекторията е непрекъсната линия, описана от точката при движението й спрямо координатната система·.

r Правоъгълна координатна система

Фиг.3 ·

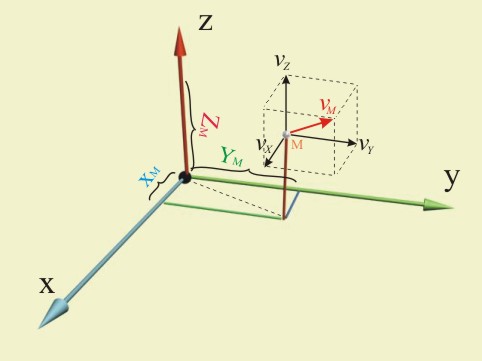
Да познаваме положението на една точка М спрямо една дадена правоъгълна координатна система означава да знаем три числа X_M, Y_M, Z_M, които дават дължините на проекциите на радиус-вектора върху трите координатни оси (фиг.3). По време на движението дължината на тези проекции се променят· - стават функции на времето (t). Така законът на движението се изразява от трите уравнения

X_M = x(t) ,

Y_M = y(t) ,

Z_M = z(t) .

Ако точката се движи така, че остава винаги в една равнина (например хОу), законът на движение се дава от две уравнения (за примера - X_M = x(t) и Y_M = y(t) ).

Ако точката се движи по права линия, то може да ориентираме оста Х успоредно на направлението на тази права, и законът на движение се дава от уравнението X_M=x(t).

При известен закон на движение, определянето на траекторията може да стане, като като се задават отделни стойности на времето t и за всяка от тях се намират съответните стойности на координатите. Така за всеки от избраните моменти се получава геометрична точка - положението на материалната точка. Въз основа на получената съвкупност от геометрични точки може да се получи траекторията, като те бъдат свързани с плавна линия&.

Уравненията от закона на движение X_M = x(t) , Y_M = y(t) и Z_M = z(t), могат да бъдат разглеждани като параметрични уравнения на траекторията с параметър времето t. Този параметър може да бъде елиминиран, така че да се получи пряка връзка между координатите на точката. Тази връзка задава една крива в координатната система. Тази крива е траекторията на движението.

В пространството кривата ще се задава от две уравнения с трите координати.

В равнината кривата ще се задава от едно уравнение с двете координати&.

Какво става, когато движението се извършва по права линия, ще трябва да се досетите сами.

r Естествена координатна система

Фиг. 4 ·

Фиг.5

Този начин за описание на движението е възможен, когато е известна траекторията. Тогава върху нея може да се фиксира една геометрична точка, и положението на движещата се материална точка да бъде определяно от едно число, което дава разстоянието (S) между двете (фиг.4). Величината се нарича "криволинейна координата" или "криволинейна абциса". В този случай законът на движение се дава от уравнението

S = S (t)

Необходимо е да се прави разлика между криволинейната координата S , която фиксира конкретното положение на точката, и изминатия път L при движението на точката по траекторията (фиг.5).