СЪДОВЕ ПОД НАЛЯГАНЕ
|
|
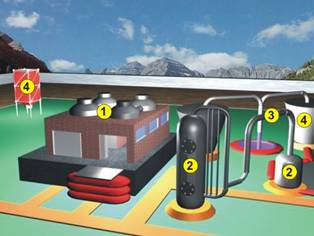
В машините и производствените инсталации
на химическата и металургичната промишленост често се срещат елементи, които не
могат да бъдат моделирани като греди или пръти. Такива са филтрите под налягане
, реакторите ‚, тръбите ƒ, резервоарите „, бутилките за сгъстен газ и
др (фиг.1). Те са изградени от тела, ограничени от две повърхнини, разстоянието
между които е малко в сравнение с останалите му размери. Тези тела се наричат
“плочи”, ако ограничаващите повърхнини са равнинни, и “черупки”, ако те са
произволни. Понататък в изложението ще
бъдат разгледани съдове, изградени от тела, околната повърхнина на които е част
от ротационна повърхнина (осовосиметрични черупки). При тези съдове се
приема, че липсват тангенциални разрезни усилия.
Осовосиметричните тела могат
да бъдат разглеждани като получени от плъзгането на една крива, която задава
меридианното направление, по окръжност (окръжностно направление).
Формирането на разрезните усилия при черупките до голяма степен зависи и от
дебелината на черупката. Когато тя е голяма, черупките се наричат
“дебелостенни” и при тях в общия случай се наблюдават всички разрезни усилия (нормални,
тангенциални, огъващи моменти). Когато дебелината е малка ( под 1/20 от радиуса
на кривина), черупките се наричат “тънкостенни” (фиг.2) и при тях огъващият
момент може да бъде пренебрегнат при определяне на напреженията и деформациите.
По-нататък в изложеиието ще бъдат разгледани
съдове, изградени от тънкостенни осовосиметрични черупки. При тези съдове
се приема, че съществуват само нормални разрезни усилия, а нормалните
напрежения са равномерно разпределени по дебелината на стената.
q Определяне
на напреженията
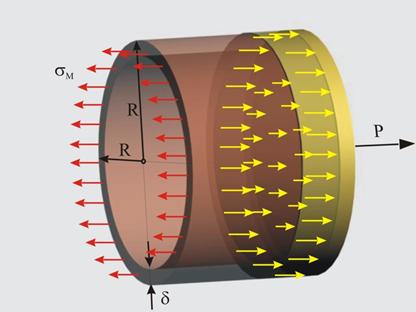
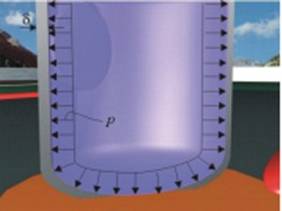
На фиг. 2 е показан разрез на
тънкостенен осовосиметричен съд, подложен на действието на налягане, равномерно
разпеделено по вътрешната стена. Дебелината на стената на съда е постоянна и е
означена с δ. В такъв случай на натоварване и геометрия се приемат следните
опростяващи предпоставки:
·
няма огъващи моменти, поради което
нормалните напрежения са равномерно разпределени по дебелината на стената на
съда;
·
нормалните напрежения в площадките,
успоредни на образуващите повърхнини бързо затихват от вътрешната стена към
външната и могат да бъдат пренебрегнати, поради което напрегнатото състояние се
приема за двумерно;
·
главните площадки са по линиите на
главните кривини (по сеченията с най-голям и най-малък радиус на кривина).
|
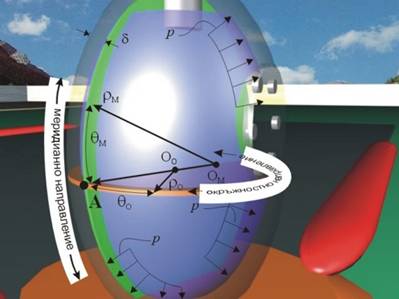
Фиг. 3 |
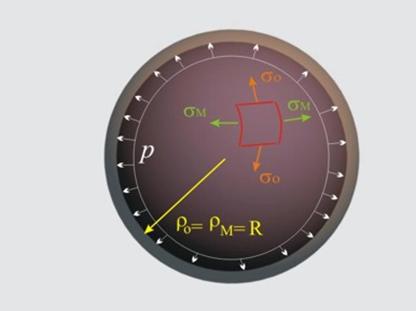
На фиг.3 направленията на главните кривини са означени като окръжностно, с радиус на кривина ρо
и централен ъгъл qO и меридианно, с радиус на кривина ρм
и централен ъгъл qм.
|
a)
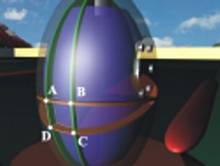
b) Фиг.4 |
Главните
напрежения могат да бъдат определени от равновесието на безкрайно малък елемент
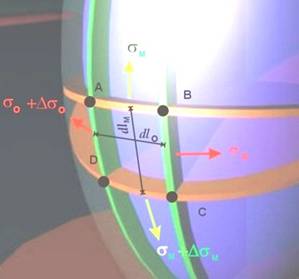
от стената на съда (фиг.4 a и b), отделен с две меридианни и две
окръжностни сечения. Страните на елемента са ориентирани по равнините на главните
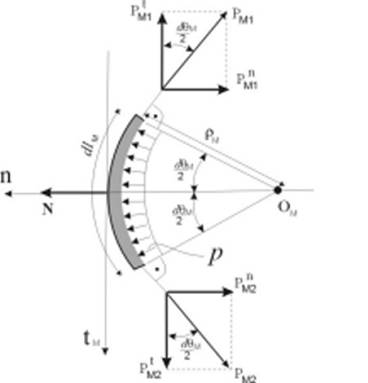
кривини. Страните АВ и CD с дължина dlo, в които
действат нормалните напрежения σM, са перпендикулярни на
меридианното направление (фиг.5).
|
|
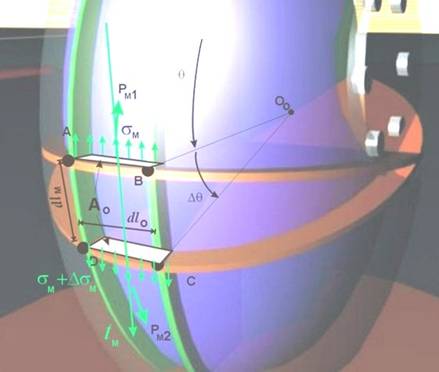
Предполага се, че нарастването на централния ъгъл DqM между двете
сечения води до нарастване на напрежението DσM. Площта на
сечението е Аo = d dlo.
Нормалните усилия в двете сечения са :
PM1 = Ao σM
= σM d dlo, (1)
за сечение АВ, и
PM2=Ao(σM+DσM)=(σM+DσM)d dlo, (2)
за сечение CD.
|
|
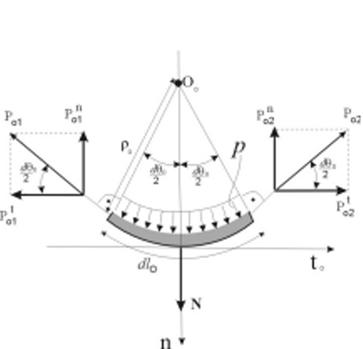
Страни BC и AD с дължина dlм, в които действат
нормалните напрежения σo са перпендикулярни на окръжностното
направление (фиг.6). Предполага се, че нарастването на централния ъгъл DqO между двете
сечения води до нарастване на напрежението DσO. Площта на
сечението е Ам = d dlм. Нормалните усилия в двете сечения са :
PО1 = AM σО
= σО d dlм, (3)
за сечение ВС, и
PО2=AM(σО+DσО)=(σО+DσО)d dlм,
(4)
за сечение АD.
|
|
Нека при тези
условия да напишем уравненията за равновесие на елемента:
-
Сумата от проекциите на силите върху
меридианното направление tM е равна на нула
(фиг.7) –
![]() ,
,
![]() ,
,
![]() ,
,
от където
DσM
= 0 и PM2 = PM1 = σM
d dlo (5)
|
|
-
Сумата от проекциите на силите върху
окръжностното направление tO е равна на нула
(фиг.8) –
![]() ,
,
![]() ,
,
![]() ,
,
от където
DσO = 0 и PO2 = PO1 = σO d dlM (6)
-
Сумата от проекциите на силите върху
нормалата е равна на нула (фиг.7 и фиг.8) -
![]() ,
,
![]() . (7)
. (7)
Силите, участващи в уравнението са:
![]() - сила, формирана от
налягане с големина р, действащо
върху елемента с площ
- сила, формирана от
налягане с големина р, действащо
върху елемента с площ ![]() ;
;
![]() - проекциите на силите
по окръжностно направление върху нормалата към елемента;
- проекциите на силите
по окръжностно направление върху нормалата към елемента;
![]() - проекциите
на силите по меридианно направление върху нормалата към елемента.
- проекциите
на силите по меридианно направление върху нормалата към елемента.
След като заместим тези стойности на силите в уравнението за равновесие
(7), получаваме:
![]() . (8)
. (8)
Като се вземе предвид, че ![]() ,
, ![]() ,
, ![]() и
и ![]() , уравнение (8) добива следния вид
, уравнение (8) добива следния вид
![]() .
.
В това уравнение може да се съкратят общите множители
![]() ,
,
![]() ,
,
и да се получи аналитичен израз за влъзката между напреженията, налягането
и геометричните размери на тънкостенния съд:
![]() . (9)
. (9)
Ако изводът на тази формула Ви се вижда сложен, постарайте се поне да
разберете и запомните следните
q
Частни случаи
|
Фиг. 9 |
·
Тънкостенен цилиндричен съд без дъно
(тръба)
При цилиндричните съдове меридианното направление е права
линия, така че радиусът на кривина е безкрайност- rM=¥ (фиг. 9).
Окръжностното направление е с
постоянна кривина, така че rо=R.
Като заместим тези стойности в уравнението за
равновесие (9), за напреженията се получава:
![]() . (10)
. (10)
|
Фиг. 10 |
·
Тънкостенен цилиндричен съд с дъно
При тези съдове налягането върху дъното формира натиск
Р = р pR2 (фиг. 10).
Този натиск се уравновесява от вътрешното усилие
N = sM 2pR d.
Като приравним двете сили, се получава
sM 2pR d = р pR2 и ![]() ,
,
от където
окончателният израз за големината на меридианното напрежение добива вида ![]() . (11)
. (11)
От уравнения (10) и (11) се вижда, че
напреженията в окръжностно направление са два пъти по-големи от тези в
меридианно. Поради това, при достигане на критичното вътрешно налягане,
разрушаването на такъв цилиндричен съд с дъно се очаква да стане от пукнатина,
успоредна на образуващата на цилиндъра (щракни тук за
анимация на процеса), предизвикана от окръжностното напрежение. Поради
това, при оразмеряването на съда, дебелината му се съобразява преди всичко с
формулата за sО.
![]() →
→ 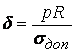
В някои случаи, за по-ефективно използване на
материала, от който е изработен съда, окръжностното направление се усилва с
пръстени (щракни тук за анимация на процеса). Това
позволява при оразмеряването на съда, дебелината му се съобразява преди всичко
с формулата за sМ и така се получава два пъти по-малка.
![]() →
→ 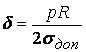 .
.
|
Фиг. 11 |
·
Тънкостенен сферичен съд
При сферичните
съдове кривините в меридианното и окръжностното направление са равни и rM = rO = R (фиг.11).
От уравнението
за равновесие (9)
![]() ,
,
за главните
напрежения се получава
![]() .
.
Вижда се, че напреженията в стените на сферичния съд при еднакви радиуси на
кривина се получават два пъти по-малки от тези в стените на цилиндричните
съдове (по окръжностно направление). Все пак, в практиката по-често се
използват цилиндрични съдове със сферични дъна, тъй като технологично са
по-лесни за изработване.

 Фиг. 5
Фиг. 5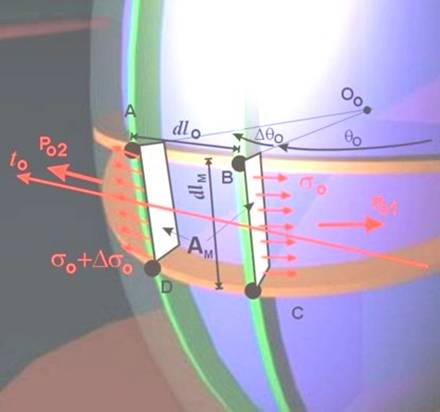 Фиг. 6
Фиг. 6