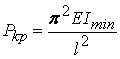УСТОЙЧИВОСТ НА НАТИСНАТИ ПРЪТИ ДО И СЛЕД ГРАНИЦАТА НА ПРОПОРЦИОНАЛНОСТ

Фиг.1

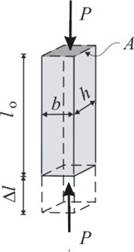
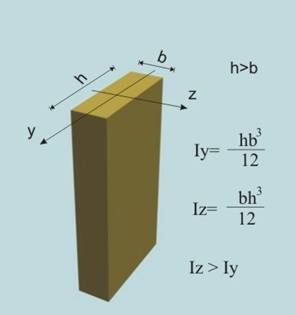
В предишна тема беше изведена формулата , по която се определят напреженията в прът, подложен на чист натиск (фиг.1). В средата на ХІХ^ти век, с широкото навлизане на желязото като конструкционен материал, напречното сечение на гредите, изчислено по тази формула, става твърде малко. Получават се "стройни" елементи, с много голяма разлика между дължината l и размерите на напречното сечение b и h. Зпочват да се случват инциденти с на пръв поглед правилно оразмерени изделия. Това предизвиква интереса на инженерите-конструктури и учените към въпросите, свързани с устойчивостта на еластичните системи, разработвани до този момент предимно теоретично. Още през средата на осемнадесети век Ойлер извежда аналитична формула за определяне големината на критичната натискова сила, при която гредата губи устойчивост и се "изкълчва". Тази формула и до днес се прилага в инженерните изчисления. Тази тема е посветена предимно на нейното получаване и прилагане.

Преди да преминем към анализа на процеса, при който една натисната греда губи устойчивост и се "изкълчва", нека да се помъчим да изясним понятието "устойчивост", видовете равновесие и как се проявяват те при натиснатите греди.

Фиг.2 ·

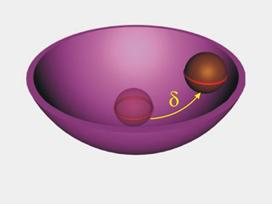
Един от начините да бъде онагледено устойчиво равновесие е състоянието на топче, поставено в паничка.

Едно тяло се намира в устойчиво равновесие, ако при малко отклонение то се стреми да се върне към равновесното си състояние и се връща към него след премахване на отклоняващото въздействие (фиг.2).

Фиг.3 ·

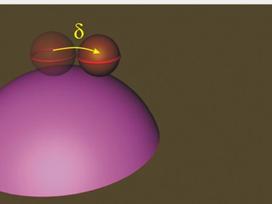
Един от начините да бъде онагледено неустойчиво равновесие е състоянието на топче, закрепено върху дъното на захлупена паничка.

Едно тяло се намира в неустойчиво равновесие, ако при малко отклонение то се стреми да продължи да се движи в посока на отклонението и след премахване на отклоняващото въздействие не се връща в изходното равновесно положение (Фиг.3).

Фиг.4 ·

Един от начините да бъде онагледено безразлично равновесие е състоянието на топче, поставено върху корава равнина.

Едно тяло се намира в безразлично равновесие, ако при малко отклонение то придобива нова форма на устойчиво равновесие (фиг.4) и за да се върне към изходното положение, към него трябва да бъде приложено отклоняващо въздействие с обратна посока ·.

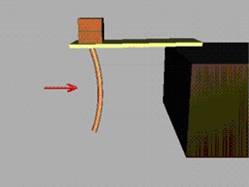
Нека сега да проследим, как тези три състояния се реализират при греда, изправена вертикално (така собственото тегло не влияе върху огъването) и натисната със сила Р ·. В примера, който се разглежда по-нататък, тази сила се формира от силата на теглото на едно тяло, поставено върху гредата и може да бъде увеличавана посредством добавяне на нови тела.

Фиг. 5 ·

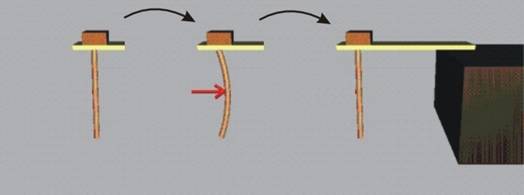
При устойчиво равновесие една смущаваща напречна сила изважда пръта от равновесното му положение, но при премахване на силата прътът възвръща равновесната си форма (фиг.5).

Устойчивото равновесие се запазва при увеличаване на натисковата сила в определени граници ·.

Фиг. 6

При увеличаване на натисковата сила прътът изпада в безразлично равновесие.

При безразличното равновесие една смущаваща напречна сила изважда пръта от равновесното му положение и при премахване на силата прътът запазва новата си криволинейна форма (фиг.6). За да възвърне първоначалната си равновесната си форма, трябва да се приложи сила с обратна посока ·.

Фиг. 7 ·

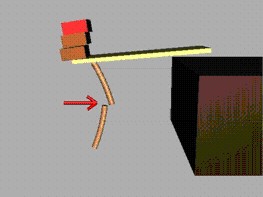
При увеличаване на натисковата сила над определена граница, която тук ще се нарича “критична сила Ркр”, равновесието става неустойчиво.

При неустойчиво равновесие една смущаваща напречна сила изважда пръта от равновесното му положение, като деформациите нарастват до разрушаване (фиг.7).

Критичната сила играе важна роля при оразмеряване и оценка на носимоспособността на натиснатите пръти. Очевидно, за да изпълняват предназначението си, те трябва да бъдат натоварени със сила, по-малка от критичната. Ако анализираме вече изработена греда с известни размери, въпросът, на който трябва да бъде даден отговор е "колко е крититичната сила?". Ако проектираме греда, която трябва да понесе известна натискова сила, въпросът, на който трябва да бъде даден отговор е "какви да бъдат размерите на напречното сечение?". И в двата случая, за да отговорим на въпроса, трябва да имаме средство за анализ, с други думи, с формула, по която да изчислим интерисуващите ни величини. Тук ще бъде предложен един прост (и поради това донякъде приблизителен) начин за изеждане на такава формула.

Фиг.8

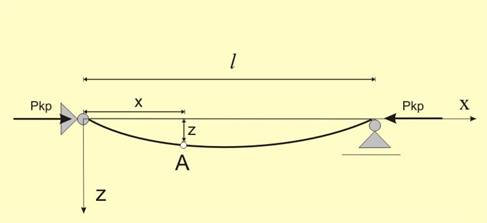
Нека да разгледаме натиснат прът, при който натисковата сила е достигнала критичната си стойност и прътът леко се е огънал (фиг.8). Както знаем, за описание на огънатата ос на гредата съществува приблизителна диференциална зависимост, известна като "диференциално уравнение на еластичната линия":

E I_min z'' = -M_ог

Това уравнение важи и за разглеждания прът. От друга страна, както се вижда от фиг.8, за дадена точка от оста на пръта (например т.А), огъващият момент е равен на

M_ог = P_kp z.

От двете уравнения се получава

E I_min z'' = -P_kp z или .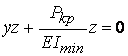

Като означим 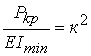, получаваме линейното хомогенно диференциално уравнение от втори ред

,

чието общо решение е z = A cos(kx) + B sin(kx).

За определяне на интеграционните константи А и В са необходими две гранични условия. Като такива могат да послужат условията в двата края на пръта.

Фиг.8

1. За левия край.

Това е началото на координатната система, следователно тук x=0 и z=0. Като заместим тези условия в общото решение, получаваме

0 = A cos(k0) + B sin(k0)=A + 0, или А=0.

Така, след прилагане на първото гранично условие, за общото решение остава

z = B sin(kx).

2. За десния край.

Тук координатата х е равна на дължината на пръта, или x=l и z=0, така че решението в тази точка се получава

B sin(kl) = 0.

Това равенство се удоволетворява във следните два случая:

1-ви случай - В=0. Тъй като вече получихме А=0, този случай води до равенството z=0, или еластичната линия съвпада с права линия - първоначалната ос на пръта. Това обаче противоречи на това, което приехме в началото - че прътът се е огънал и оста му е крива линия. Поради това този случай не представлява интерес за изследването.

2-ри случай - sin(kl) = 0. Това условие се изпълнява, когато kl приема стойностите kl=0,p , 2p, 3p,…np, където n е цяло число. За общия случай kl=np, откъдето .

Да си спомним, че по полагане 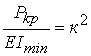. Като обединим този израз с резултата от горния ред, получаваме:

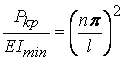
и

.

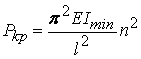По това уравнение, като заместваме различни стойности на n, ще получаваме различни стойности на критичната сила. От практическа гледна точка, интерес представлява най-малката от тези стойности, която все пак да не е нула. Тази стойност се получава при n=1 и е

.

Така се получава формулата на Ойлер, за която вече стана дума. При нейното прилагане трябва да се съблюдават следните три важни особености, пренебрегването на които може да доведе до катастрофално грешни резултати:

Фиг.9 ·

r Формулата се прилага с минималния инерционен радиус

Това правило произхожда от необходимостта да бъде получена най-малката стойност на критичната сила. Например, ако прътът има правоъгълно напречно сечение, така че главните инерционни моменти не са равни, то огъването при загуба на устойчивост ще стане в равнината на по-малката коравина, или гредата ще се завърти около тази ос, спрямо която напречното сечение има най-малък инерционен момент (фиг.9). Едно подръчно средство, с което може да се демонстрира тази особеност е чертожната линийка, който лесно се огъва в една равнина и е почти невъзможно да бъде огъната в друга равнина, перпендикулярна на първата.

r Критичната сила се влияе от начина на закрепване

Схемата от фиг.8, която беше използвана при извода на формулата на Ойлер, е прът, ставно подпрян в двата си края. Има голямо разнообразие на начините на закрепване на прътите в една конструкция. Влиянието на тези начини се взима предвид във формулата посредством промяна на дължината l с коефицента b в една обобщена формула

.

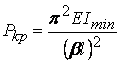Изразът s=(bl) се нарича "приведена дължина" и е равна на една полувълна от деформираната ос на пръта

Тук ще бъдат разгледани четири основни случая на закрепване

Фиг.10 ·

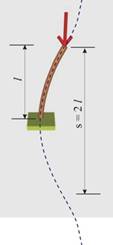
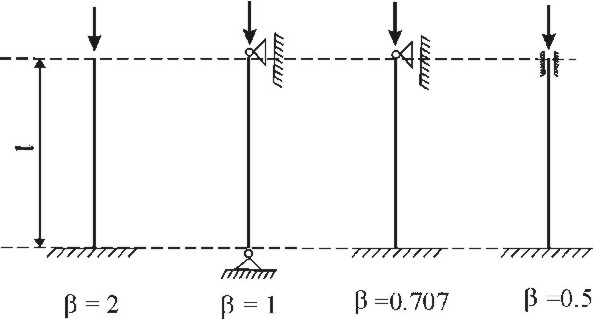
1. Запъване в единия край и свободен втори край - b = 2 (фиг.10)

Фиг.11 ·

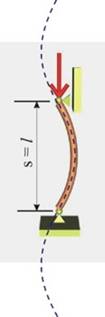
2. Ставно подпиране в двата края - b = 1 (фиг.11)

Фиг.12 ·

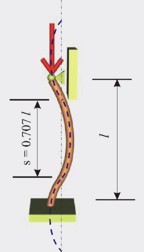
3. Ставно подпиране в единия край и запъване в другия - b=0.7 (фиг.12)

Фиг.13 ·

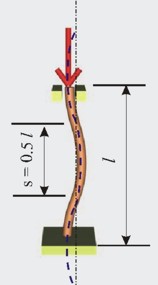
4. Запъване в двата края - b=0.5 (фиг.13)

Едно обобщение на четирите случая е представено на фиг.14

r Формулата на Ойлер важи само за елементи, чиито материал работи в участъка под границата на еластичност.

Тази особеност произхожда от факта, че изводът на диференциалното уравнение на еластичната линия, което беше използвано, е направен при предпоставка за валидност на закона на Хук. За да се определи в коя част на деформационната диаграма попада конкретно решение (под границата на еластичност или над нея) се въвежда характеристиката "стройност на пръта" - 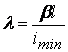, където i_min е минималният инерционен радиус 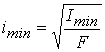(F- площ на напречното сечение).

За определяне на условията за устойчивост над границата на еластичност има различни методи, залегнали в нормативните документи (стандарти). Ако добре усвоите изложената до тук теория, важаща за еластичната област, със сигурност ще се справите, ако това се наложи в конкретен случай, с литературата, касаеща проблема извън тази област.