УСУКВАНЕ
Материалът
e разработен
с помощта на Гергана
Иванова (ЕК 282) от
кръжока по
Техническа
механика
1. Тангенциални
напрежения
при усукване
на вал с
кръгло
напречно
сечение
Когато
в напречното
сечение от
възможните
шест
разрезни
усилия
действа само
усукващият
момент Мх,
материалът
оказва
съпротива на
усукване. На
такава
съпротива са
подложени
конструкционни
елементи,
наречени
“валове”,
които предават
въртящ
момент.
|
Фиг.1 |
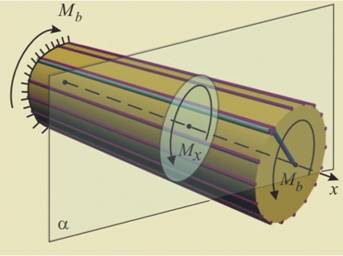
Един
пример на вал
с кръгло
напречно
сечение е
показан на
фиг.1 ·.
Върху десния
свободен
край на вала
е приложен
съсредоточен
въртящ
момент около
оста х, който
валът
предава на
опората в
левия край.
Ако направим
разрез на
вала с
равнина a,
перпендикулярна
на оста му,
единственото
разрезно
усилие, което
ще се формира
от външния
въртящ
момент Mb, е
усукващ
момент Мх.
Необходимо е
да бъде
изведен
изчислителен
апарат за
определяне
на
напреженията,
които това
разрезно
усилие ще
предизвика.
|
Фиг.2 |
За
да се
илюстрира
формирането
на междучастичните
сили при този
вид външно
въздействие,
гредата се
представя
като
съставена от
множество
тънки дискове,
притиснати
един към
друг.
Въртящият
момент се
стреми да
завърти
дисковете като
ги плъзне
един спрямо
друг ·.
На това
завъртане
противодействат
сили на
триене,
действащи в
повърхнините,
по които
дисковете
контактуват ·.
Като
аналог на
дисковете от
модела, в
реалните
тела могат да
бъдат приети
отделните слоеве
на
частичките,
които
изграждат
материала на
изделието. Тогава
аналог на
силите на
триене ще
бъдат междучастичните
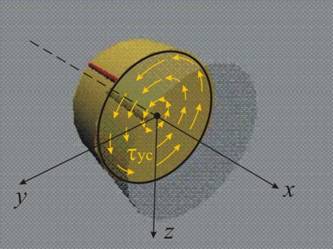
сили. Тези
сили лежат в
равнината на
направеното
сечение и се
представят с
тангенциални
напрежения t ус (“ус” –
усукване,
фиг.2).
За да
намерим
разпределението
на напреженията
в точките от
напречното
сечение,
отстоящо на
дадено
разстояние х
от левия край
на вала, ще
използваме съществуващата
от закона на
Хук
зависимост
между
тангенциалното
напрежение t и ъгловата
деформация g (физична
страна на
проблема):
|
Фиг.3 |
В
този израз
коефициентът
G е
материална
характеристика
и се смята за известен
– определен
при
експериментално
изследване
на материала.
Така, за да
бъде
определено
напрежението,
остава да
бъде
определена
ъгловата
деформация g. За целта ще
проследим
процеса на
деформиране
на гредата
(вала) при
усукване (геометрична
страна на
проблема) ·.
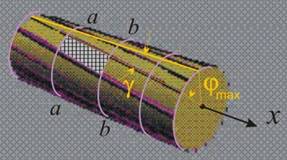
Върху
повърхнината
на вала, преди
да бъде
натоварен, е
нанесена
ортогонална
мрежа,
образувана
от прави
линии, успоредни
на оста х, и от
перпендикулярни
на тях
окръжности
(фиг. 3а). След
натоварването
се
установява
(фиг. 3б), че
окръжностите
запазват
вида си,
докато правите
линии се превръщат
във винтови
линии.
Правоъгълните
преди
натоварването
елементи
(един от тях е
защрихован
на фиг. 3а) се
преобразуват
в
успоредници (фиг. 3б).
Такова
поведение на
деформация
ще има един
модел на вал,
състоящ с от
корави
дискове (напречни
сечения), които
при
натоварването
на вала се
завъртат
един спрямо
друг, без да
се
изкорубват (депланират).
Така на фиг. 3б
свободният
край на вала,
т.е.
най-дясното
му сечение се
завърта
спрямо
неподвижно
запънатото
сечение на
ъгъл jмах.
Ъгълът на
наклона на
винтовите
линии е
постоянен и
представлява
изменението
на правия
ъгъл, т.е е
равен на
ъгловата
деформация g.
Ще
припомним, че
подобно
допускане за
равнинност
на
напречните
сечения при
настъпилите
деформации,
използвахме
и при опън (натиск).
Това беше
хипотезата
на Бернули.
Разбира се,
при опън
(натиск) оставащите
равнинни
(плоски)
напречни
сечения се
изместват по
направлание
на оста х, докато
пи
усукването
те се
завъртат
около нея без
да променят
разстоянията
помежду си.
Експериментът
показва, че
хипотезата
на Бернули не
е валидна при
всички форми
на напречно
сечение на
вала.
Например,
усукването
на вал с
правоъгълно
сечение е
свързано с депланация
на
напречното
сечение.
Хипотезата
може да бъде
приета при
валове с
напречно
сечение кръг
или кръгов
пръстен
(тръбовидно
сечение).
|
|
Като
се използва
хипотезата
за равнинните
сечения, ще
може да се
намери
деформационното
условие при
често
усукване. За
целта се
разглежда
безкрайно
малкия
елемент от вала,
заключен
между
сеченията а и b
(фиг.3 и фиг.4).
Сечението а,
отстоящо на
разстояние х от
мястото на
запъването
се завърта на
ъгъл j,
наречен ъгъл
на усукване.
Сечението b,
отстоящо на
разстояние dх
от
а е завъртяно
спрямо
неподвижното
сечение на
ъгъл j+dj, т.е. ъгълът
на завъртане
на b спрямо а е dj. На фигурата
е показан и
постоянния
ъгъл на
наклона g на една от
винтовите
линии,
изобразени
на фиг. 3б.
На
фиг. 5
безкрайно
малкият
елемент на
вала, заключен
между двете
сечения а и b е
показан
отделно.
Точките А и В
са от правата
линия,
нанесена
върху
повърхността
на вала преди
натоварването
му. След натоварването,
тази права
става
винтова линия,
като за
разглеждания
безкрайно
малък елемент,
това е
правата AD, наклонена
под ъгъл g. В
правоъгълния
ΔABD дъгата
BD може да
бъде приета
за катет и да
бъде
изразена като:
BD = AB tgg (2)
Същата
дъга може да
бъде
изразена и
като дъга с
централен
ъгъл dj от
сечението b с
радиус r:
BD = r dj .
(3)
Като
се вземе
предвид, че
АВ= dх и че
за безкрайно
малък ъгъл g може да се
приеме tgg»g, от (2) и (3)
следва, че
AB tgg = r dj , dх g = r dj и ![]() . (4)
. (4)
Изразът
![]() представлява
ъгъл на
усукване за
единица
дължина от
вала и се
нарича
представлява
ъгъл на
усукване за
единица
дължина от
вала и се
нарича
относителен
ъгъл на
усукване q, т.е.:
Така
от (4) и (5)
получаваме g=r q.
(6)
Като
се замести
изразът (6) (получен
при анализ на
геометричната
страна на
проблема)
в израза (1) (от
физичната
страна на проблема),
се получава:
Полученият
израз може да
бъде
използван за
изчисляване
на
напреженията,
само ако е известен
относителният
ъгъл на
усукване q.
Този ъгъл
може да бъде
определен от
третата, статична
страна на
проблема. Тя
се изразява в
положението,
че редукцията
на
напреженията
в точките от
сечението спрямо
оста х има
за резултат
само един
момент, който
трябва да
бъде равен на
усукващия
момент dМх.
|
|
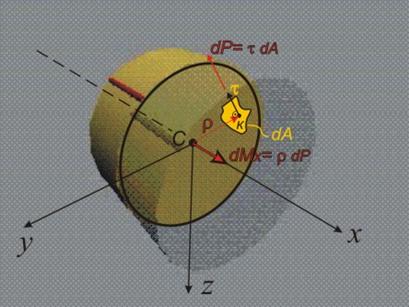
На
фиг.6 е
показан
безкрайно
малкия
елемент с
лице dА,
описан около
т.К,
намираща се
на
разстояние ρ
от центъра С
на напречното
сечение.
Тангенциалното
напрежение,
действащо в
безкрайно
малката
околността
на т.К, формира
безкрайно
малка сила
Р= t dА. (8)
Тази
сила формира
спрямо оста х
безкрайно
малък момент
d Мх = r dР. (9)
Пълният
момент на
напрежението
в цялото
сечение се
получава,
като изразът
от (9) се
интегрира по
цялата площ
на сечението:
![]() ,
,
и
окончателно
![]() . (10)
. (10)
|
Фиг.7 |
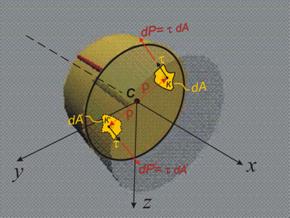
Поради
осовата
симетрия, на
всяка
елементарна
площ dА
може
да се намери
съответстваща
площ dА/,
намираща се
от другата
страна на т.С
(фиг.7). В тази
площ
напрежението
ще формира
елементарна
сила dР/, равна
по големина
на dР, но с
противоположна
посока, така
че dР+ dР/=0.
В резултат
за главния
вектор при
редукцията
ще се получи ![]() .
.
Като
се замести (7) в
(10) се получава:
![]()
Интегралът
![]() представлява
полярен
инерционен момент
за т.С, така че
за усукващия
представлява
полярен
инерционен момент
за т.С, така че
за усукващия
момент
се получава:
![]() ,
,
от където
Сега вече е
възможно ур.7
да бъде
използвано
за
определяне
на
напреженията,
след като относителният
ъгъл на усукване
бъде
заместен по
ур.11:
t = G r ![]() ,
или t =
,
или t = ![]() .
(12)
.
(12)
В
последната
зависимост IC е геометрична
характеристика
на сечението.
За кръгло
напречно
сечение с
диаметър D се
получава, че
|
Фиг. 8 |
IC=![]() .
.
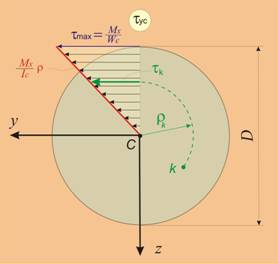
От
(12) следва,
че
тангенциалното
напрежение t в дадена
точка от
сечението е
линейна
функция на
разстоянието
ρ на точката
до центъра на
сечението. На
фигури 8а и 8б са
показани
диаграмите
на
тангенциалните
напрежения
при кръг и
при кръгов
пръстен.
Най-голямото
значение за
напрежението
се получава в
точките от
контура на
сечението, за
които
ρ= ρмах=D/2. При
тях
където
WC = ![]() е също
една
геометрична
е също
една
геометрична
характеристика
на сечението,
наречена полярен
съпротивителен
момент.
При
кръгло
напречно
сечение с
диаметър D за полярния
съпротивителен
момент се
получава
WC= ![]()
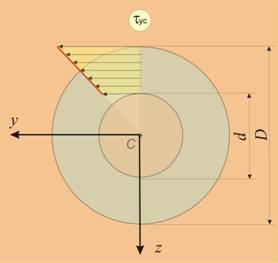
При
напречното
сечение
кръгов
пръстен (фиг. 8б) имаме
WC=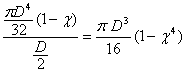 , където
, където ![]()
·
Деформация
на вал с
кръгло
напречно
сечение;
·
Якостно и
деформационно
условие при
усукване на
вал.
Оразмеряване.

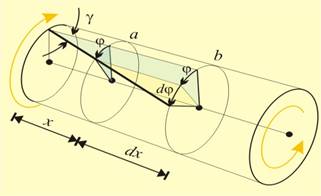 Фиг.4
Фиг.4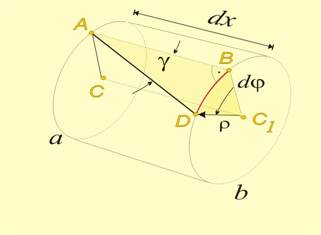 Фиг.
Фиг.