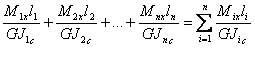Деформация на вал с кръгло напречно сечение

Материалът e разработен с помощта на Гергана Иванова (ЕК 282) от кръжока по Техническа механика

В предишен материал се установи, че относителният ъгъл на усукване q се дава от следния израз:

q = .

Ъгълът на усукването φ може да бъде получен, като се вземе под внимание изразът (5) от същия материал, т.е.

q =

От двете уравнения получаваме:

q = = ,

от където dφ = (1)

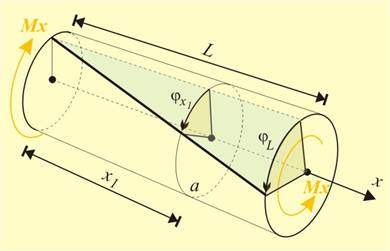
Фиг.1

Уравнение (1) се нарича диференциално уравнение за усукване на вал с кръгло напречно сечение. Чрез неговото интегриране може да се определи ъгълът на усукване за произволно сечение от вала, спрямо друго избрано сечение. Например (фиг.1), ъгълът на усукване на сечението а, отстоящо на разстояние х₁ от най-лявото неподвижно сечение на вала ще бъде

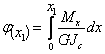
Ако в даден участък 0≤х≤L, усукващият момент е постоянен и напречното сечение, съответно I_C не се изменя (както е случаят на фиг.1), то те могат да бъдат извадени пред интеграла, така че се получава:

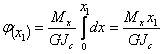и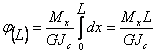

На фиг.1 j_(L)= j_мах, т.е. това е ъгълът на усукване на крайното дясно сечение на показания вал.

Произведението G I_C се нарича коравина при усукване, аналогично на коравината при опън ЕF.

Ако имаме вал с дължина L и няколко участъка, всеки един с дължина l_i като във всеки участък съответните усукващи моменти М_iх и коравини G_iI_ic=GI_ic са постоянни, ъгълът на завъртане на крайното дясно сечение, спрямо крайното ляво сечение ще се намери по формулата (фиг.2):

φ_(L) = (2)

В това уравнение усукващите моменти трябва да се заместват с алгебричните им стойности, взети от М_х – диаграмата.

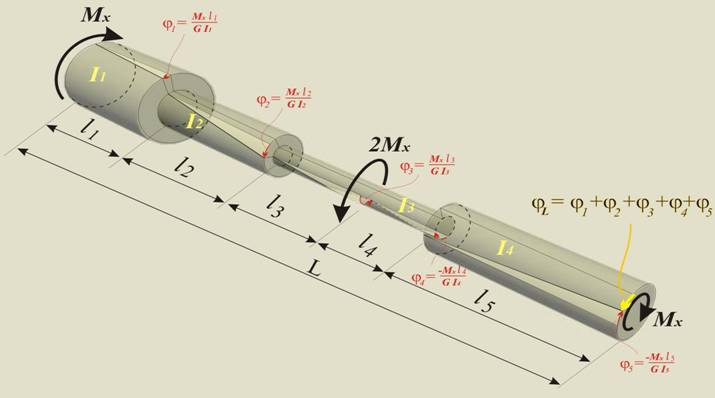Фиг.2