Напрежение
и деформация
при опън и
натиск.
Понятията
“опън” и
“натиск” са
добре
познати от
ежедневната
практика. В
техническата
механика се
казва, че
телата са
подложени на такова
въздействие,
ако
нормалното
разрезно
усилие N е
различно от
нула. Aко освен
това другите
разрезни
усилия са
нула (Qy=0, Qz=0, Mx=0, My=0, Mz=0), тялото
е
натоварено
на чист опън
(при N >0), или
на чист
натиск (при N <0).
Деформации
при опън и
натиск – бяха
разгледани в
предишен
параграф Ã.
Напрежения
при опън и
натиск.
|
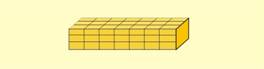
Фиг.1 · |
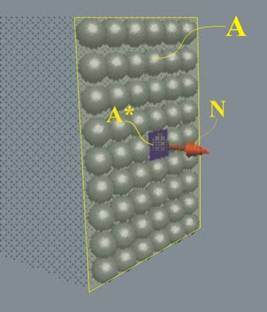
Ако
на
повърхността
на
призматично
тяло бъде
нанесена
мрежа от
взаимно-перпендикулярни
линии,
успоредни на
ръбовете на
тялото, и
тялото бъде
натоварено
на опън, може
да се
забележи, че
в новото,
деформирано
състояние на
тялото
линиите от
мрежата
остават
взаимно-перпендикулярни
(фиг.1).
Поради
това може да
се
предположи,
че равнинните
сечения на
тялото,
перпендикулярни
на оста, по
която е
приложена
силата в
недеформирано
състояние,
остават
равнинни и в
деформирано
състояние
(хипотеза на
Бернули).
Запазването
на правия
ъгъл между
линиите говори
за липса на
ъглови
деформации и
тангенциални
напрежения Ã. В
тялото се
формират
само
нормални
напрежения,
които при
определени
условия
могат да
бъдат приети
за
равномерно-разпределени
в напречното
сечение на
тялото.
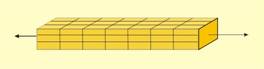
|
Фиг.2 · |
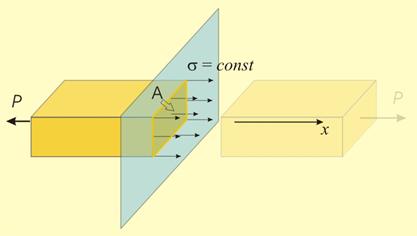
Тези
условия са
(фиг.2):
1.
Директрисите
на
приложените
сили да съвпадат
с оста на
тялото
(центричен
опън или
натиск).
2.
Разглежданото
сечение да е
достатъчно
отдалечено
от местата,
където са
приложени външните
сили.
3.
Разглежданото
сечение да е
достатъчно
отдалечено
от опорите.
4.
Разглежданото
сечение да е
достатъчно
отдалечено
от местата,
където има
рязка промяна
(скок) на
размерите на
напречното
сечение.
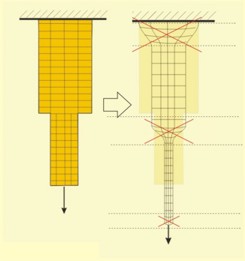
|
Фиг.
3
Фиг.4 |
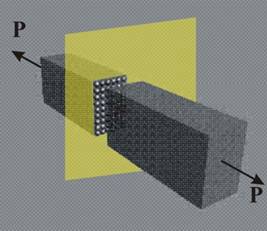
Напрежения
в площадки,
нормални на
оста на гредата
На
микро ниво се
наблюдава
промяна на
разтоянията
между
центровете
на тежестта
на частичките
така, че
структурните
частички във
вътрешността
на гредата
също остават
в една и съща
равнина ·.
Големината
на
нормалните
напрежения
може да бъде
определена
от локалното
равновесие
на част от
тялото,
отделена с
равнина, перпендикулярна
на
надлъжната
ос ·. Според
хипотезата
на Бернули,
междучастичните
разтояния ще
се променят
равномерно
за всички
частици от
сечението и
ще формират
еднакви сили
на отцепване (N) на
междучастично
взаимодействие
·. Тъй
като няма движение
на частиците
успоредно на
разглежданата
равнина,
тангенциалната
сила на плъзгане
ще бъде равна
на нула.
За
една
разглеждана
частичка ·,
силата на
отцепване ще
формира
нормално напрежение ![]() ,
,
където
А*
е площта на
тази част от
сечението,
която е присъединена
към
частицата. В
този израз може
да умножим
числителя и
знаменателя
с броя (n)
на
частичките в
сечението,
без да
променяме
стойността
на
напрежението:
|
Фиг.
5 |
![]() .
.
Така
в числителя
се получава
сумата от
всички сили
на отцепване,
действащи
върху частичките
от сечението ·. Тази
сума е равна
на силата Р,
действаща
върху
гредата ·.
В
знаменателя
се получава сумата
от частите на
сечението,
присъединени
към всички
частички.
Тази сума е
равна на
площта А
на сечението
на гредата.
Така за
напрежението
се получава:
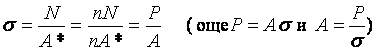 ,
фиг. 5.
,
фиг. 5.
Напрежения
в площадки,
наклонени
спрямо оста
на гредата
Равнината,
нормална на
оста на
гредата, не
е
единствената
равнина, по
която може да
се направи
анализ на
взаимодействието
на разглежданата
частичка с
останалите
частички на
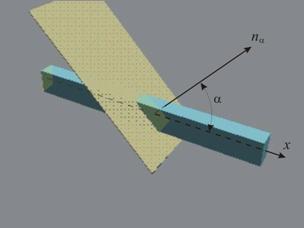
гредата. През
същата
частичка може
да бъде
прекарана и равнина , чиято
нормала не
съвпада с
оста на
гредата, а
сключва с нея
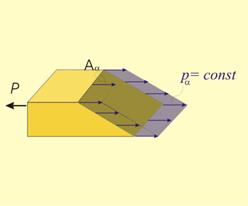
ъгъл a (фиг.6) ·.
|
|
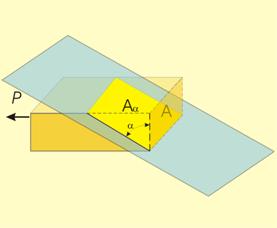
Площта
(Аa)
на новото
сечение ще
бъде
по-голяма от площта А
на
нормалното
сечение (фиг.7):
![]() .
.
Тъй
като за тази
площадка
напрежението
е наклонено
спрямо
нормалата (не
е нито само нормално,
нито само
тангенциално),
то се
отбелязва с (рa) и се
изчислява
като:
![]() , а като
заместим Аa с
неговото
равно, и като
, а като
заместим Аa с
неговото
равно, и като 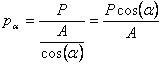 .
.
Сега може ![]() да
бъде
заместено с
да
бъде
заместено с
напрежението
в нормалната
площадка и да
бъде
направена
връзка между
двете
напрежения:
![]() .
.
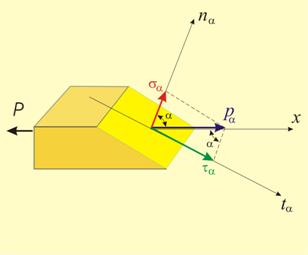
Напрежението може да
бъде
разложено по
основните
направления
на
площадката и
така да бъдат
получени
нормалната · и
тангенциалната
· компонента
на
напрежението
(нормалното
напрежение sa и
тангенциалното
напрежение ta, фиг.9):
![]() ,
,
![]() .
.