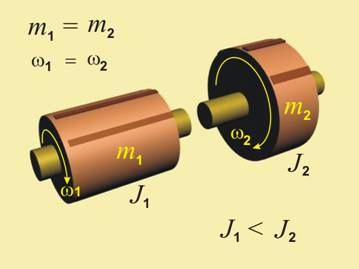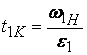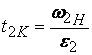ТЕОРЕМА ЗА КИНЕТИЧНИЯ МОМЕНТ НА МАТЕРИАЛНА СИСТЕМА
Пример №1 Ротационно движение на диск
Нека да разгледаме два диска с еднаква
маса, но с различен радиус, движещи се ротационно с хоризонтална ос на въртене
(фиг.1). Въпреки че масите на двата диска са равни, те ще имат различни масови
инерционни моменти. Масата на диска с по-голям радиус е разпределена на
по-голямо разстояние от оста на въртене, и поради това, този диск ще има
по-голям инерционен момент.
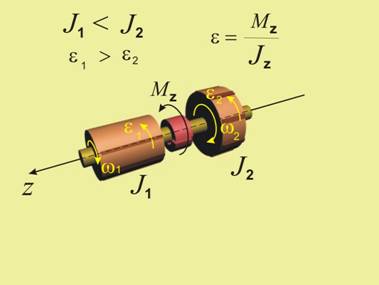
Нека сега да предположим, че
посредством някакво техническо средство (например челюстна спирачка) създаваме
външен момент, обратен на посоката на въртене (фиг.2). Според теоремата за кинетичния
момент,
®
и окончателно: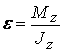 
,
или приложеният момент ще създаде ъглово ускорение e със същата посока, като на момента - обратна на
въртенето. Поради това за ъгловата скорост ще имаме:
,
и като интегрираме между два момента - начален (н) и краен (к), получаваме:
.
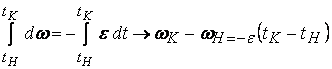Нека започнем измерването на времето от началния момент (tH=0), в който
дисковете се въртят с ъглова скорост wН=w1=w2, а вторият
момент да бъде момента, в който дискът спира движението си (wК=0).
Тъй като масовият инерционен момент на първото
тяло от фигурата е по-малък от инерционния момент на второто тяло ® J1<J2, то от
формулата 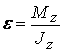следва, че ъгловото
ускорение на второто тяло ще бъде по-малко от ускорението на първото ® e2<e1. Като
заместим тези величини в уравненията за двете тела, получаваме:
|
Парво тяло |
Второ тяло |
|
|
|
|
И тъй като wН1=wН2 и e2<e1, то следва, че: t2K > t1K (второто тяло ще спре за по-дълго
време от първото ·) |
|
