КИНЕМАТИКА НА ТРАНСЛАЦИОННО ДВИЖЕНИЕ НА ТЯЛО

Едно тяло се движи транслационно, когато всяка права, свързана с тялото, остава успоредна сама на себе си по време на движението.

Фиг.1 ·

Фиг.2

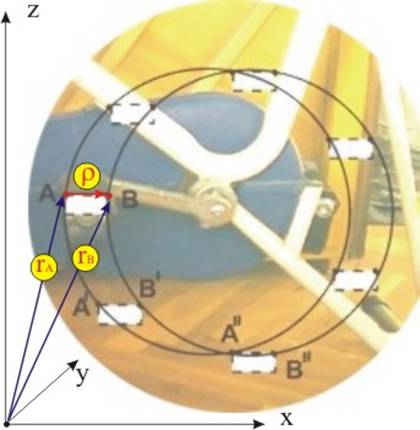
Напремер педалът на велосипеда от фиг.1 извършва транстлационно движение, тъй като осечките АВ, А’В’, А’’В’’ и т.н. са успоредни, а т.А и т.В се движат по еднакви траектории, успоредно отместени една спрямо друга.

При транслационното движение скоростите и ускоренията на всички точки от тялото са равни. Така движението е напълно определено, ако се познава движението само на една негова точка (например т.А).

Нека да означим радиус-векторът на т.А с r_A. Радиус-векторът на всяка друга точка от тялото (например т.В) може да се изрази с r_A и разстоянието r (Фиг.2):

r_В = r_A + r .

Тъй като тялото е идеално-твърди (недеформируемо), разстоянията между точките остават постоянни по време на движението. Това означава, че векторът r е постоянен по големина и направление (за направлението - поради транслационното движение).

Или r = const. (не зависи от времето)

Така излиза, че ако познаваме законът на движение на т.А r_A=r(t), можем да определим законът на движение и на т.В (или на всяка друга точка) r_В = r(t) + r .

Нека да определим скоростта на т.В като диференцираме законът за движение по времето:

.

Тъй като и , то окончателно се получава V_B=V_A.

От равенството на скоростите следва и равенство на ускоренията:

.

При задачите за транслационно движение на тяло, вместо да се разглежда движението на тялото, се изучава само движението на една негова точка, или задачата се свежда до решаване на задача от кинематика на точка.