СПЕЦИАЛНО ОГЪВАНЕ

Разпределение и големина на тангенциалните напрежения

Терминът “чисто специално огъване” показва, че външните сили създават в гредата само един огъващ момент Ã.

Терминът “специално огъване” (без определението “чисто”) показва, че външните сили създават в гредата не само огъващ момент М_у (един, поради което остава терминът “специално”), а и тангенциално разрезно усилие Q_z.

Действието на огъващия момент и в този случай поражда нормални напрежения, които се определят както в случая на чисто специално огъване Ã. По-нататък ще бъде анализирано само действието на тангенциалното разрезно усилие.

Фиг.1

Фиг.2

Фиг.3

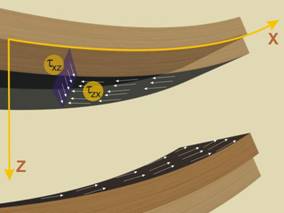
Един подходящ начин за онагледяване на въздействието, което тангенциалното разрезно усилие Q_z оказва върху гредата, е тя да бъде представена като съвкупност от тънки пластини, подредени една върху друга и притиснати така, че да образуват едно цяло (фиг.1), но деформиращи се всяка сама за себе си · (фиг.2). За такъв “пакет” един положителен момент скъсява горните нишки на всяка пластина и удължава долните.

На местата, където пластините контактуват (например пластините  и ‚, фиг.3) се събират опънатите и удължени нишки на горната пластина (оцветени в синьо) и натиснатите и скъсени нишки на долната (в червено). Това довежда до плъзгане на пластините една спрямо друга при огъването на целия пакет.

Фиг.4

Фиг.5

Фиг.6

Фиг.7

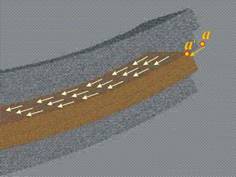
Този процес може да се опише така: В изходното, недеформирано състояние, точките по контактните повърхности на пластините са общи (например т.а, фиг.4). При огъването на пакета, всяка пластина се деформира самостоятелно, точките се разделят и пластините се плъзгат една спрямо друга · (в случая на разстояние а-а’, фиг.5).

Плъзгането довежда до формиране на сили на триене Ã.

В една хомогенна греда ролята на пластини играят слоевете, образувани от частиците на материала, а на сили на триене – междучастичните сили. Тъй като тези сили действат в равнините на плъзгане, те се представят с тангенциални напрежения (фиг.6). Напреженията действат в равнини, нормални на оста z и са насочени по направление на оста х, поради което се означават като t_zx.

По принципа за съответствие на тангенциалните напрежения в две взаимно-перпендикулярни площадки, в гредата ще се формират и тангенциални напрежения t_xz = t_zx (фиг.7).

Фиг.8

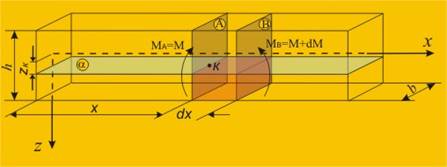
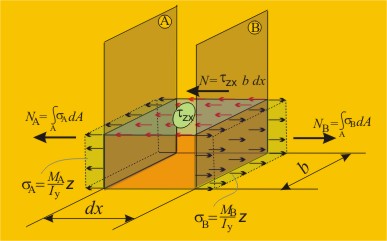
Напреженията в една произволна т.к, отстояща на разстояние z_k от неутралната линия, може да бъдат определени от локалното равновесие на елементарна част от гредата около точката, ограничена от равнината на плъзгане a и две сечения и , отстоящи на разстояние dx (фиг.8). Предполага се, че в лявото сечение действа огъващ момент М_А=М. Този момент ще предизвика напрежения (фиг.9). Равнодействащата на тези напрежения може да се получи, като напреженията се интегрират за площта А на сечението ® . Моментът и инерционният момент са постоянни за

сечението и могат да бъдат изведени пред интеграла: . Това, което остава под интеграла е статичен момент на сечението спрямо оста у: , така че за равнодействащата се получава

Фиг.9

, или . (1)

Съответно за дясното сечение:

.

Тъй като за дясното сечение има нарастване на координатата с dx, то и моментът също ще се промени, или: М_В=М+dM. Така за равнодействащата на напреженията в това сечение се получава:

. (2)

Долната страна на разглежданата част от гредата е свободна от натоварване, което значи, че е свободна и от напрежения. Върху горната страна действат тангенциални напрежения t_zx (страната е перпендикулярна на оста z, а напреженията са насочени по оста x). Равнодействащата на тези напрежения се получава, като ги умножим по площта върху която действат:

Т = t_zx b dx. (3)

И така, установи се, че върху разглежданата част от гредата действат три хоризонтални сили. По принципа на локалното равновесие, сумата на трите сили трябва да бъде нула (знаците на силите се определят спрямо оста х, която е насочена на дясно):

- N_A –T + N_B = 0.

Като се заместят в това уравнение изразите от (1), (2) и (3), се получава:

,

или като се съкратят еднаквите изрази с противоположни знаци:

. (4)

От уравнение (4) тангенциалното напрежение може да бъде изразено като:

.

От диференциалните зависимости при разрезните усилия се знае, че . Като се вземе предвид и правилото за съответствие на тангенциалните напрежения, окончателно се получава:

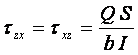. (5)

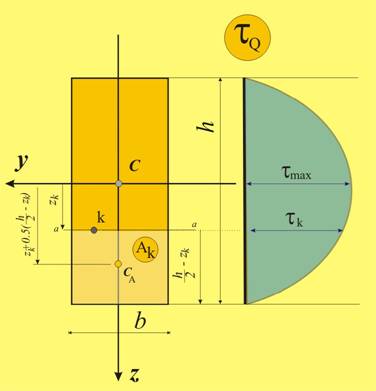
Уравнение (5) се нарича “формула на Журавски за тангенциалните напрежения”. В тази формула Sy се замества със статичния момент на тази част от напречното сечение, която е отделена с права, минаваща през точката и успоредна на оста у (правата а-а от фиг.10). Тъй като правата дели напречното сечение на две части, за да има съответствие с избраната част от гредата на фиг.8 и фиг.9, сега избираме тази част, която не включва оста у (долната част от фиг.10).

Фиг. 10

Както е известно, статичният момент на тази фигура е равен на произведението от площта (в случая Ак) и разстоянието от центъра на тежестта С_А на фигурата до оста у (в случая , фиг.10). Или:

,

и тъй като

,

окончателно

,

и 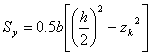. (6)

От уравнение (6) се вижда, че докато останалите членове от формулата на Журавски не зависят от местоположението на точката, то статичният момент зависи посредством координатата си z – статичният момент е квадратна парабола на z. Когато (т.к е на долния ръб на гредата), изразът в скобите на ур.6 става нула, от където и статичният момент е нула. Същото се получава и при (т.к е на горния ръб на гредата).

Фиг.11

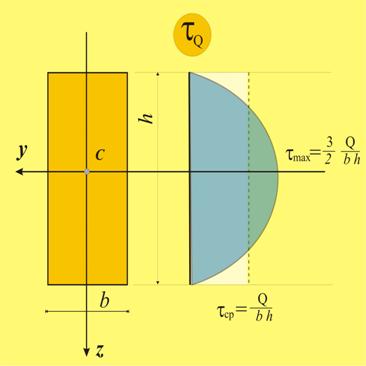
Най-голяма стойност изразът в скобите, а от там и статичния момент, има при z=0. По същия начин, чрез статичния момент, координатата z влияе и върху тангенциалното напрежение. Разпределението на тангенциалното напрежение е показано на фиг.11. Максималното напрежение ще бъде:

®,

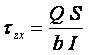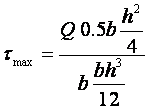и след като се направят съкращенията:

.

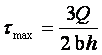Ако положим 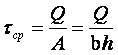, за максималната стойност се получава (фиг.11):

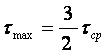. (7)

Трябва да се отбележи, че ур.7 е вярно само за греди с правоъгълно напречно сечение. Например за кръгло сечение .

В практиката често се срещат греди, чието напречно сечение е правоъгълно, но с променлива ширина. Един приблизителен анализ на разпределението на напреженията в този случай може да бъде проведен по следния начин:

Фиг. 12

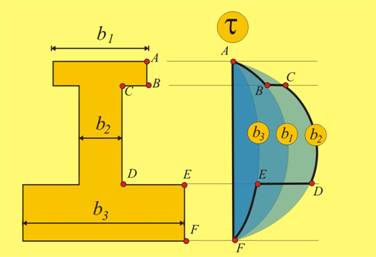
На фиг. е показано напречно сечение на греда, което обикновено се нарича “двойно Т^е”. То се състои от горен пояс с ширина b₁, стебло с ширина b₂ и долен пояс с ширина b₃. Като се заместят поотделно трите ширини във формулата на Журавски, ще се получат три различни разпределения на тангенциалното напрежение (по-малка ширина – по-голямо напрежение, фиг.12). Кривата на действителното напрежение A-B-C-D-E-F се получава, като в рамките на всеки участък се вземе съответното разпределение (A-B, C-D, E-F), а в точките където има преход от една ширина към друга, кривата скача от едно разпределение на друго (B-C, D-E, фиг.12).