ЧИСТО СПЕЦИАЛНО ОГЪВАНЕ

Разпределение и големина на нормалните напрежения

Фиг.1

В заглавието на тази тема има два термина, които трябва да бъдат пояснени, преди да се премине към анализа на явлението.

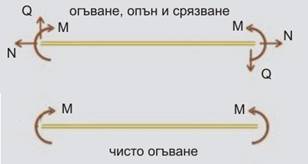
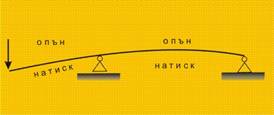
- Чисто огъване има тогава, когато върху гредата действат само огъващите моменти (фиг.1). Както вече видяхме, тези моменти са два - Му (фиг.2) и Мz (фиг.3).

Фиг. 2 кликни върху картинките за анимация Фиг. 3

- Специално огъване има тогава, когато действа само единият от двата момента. В случайте, които ще разгледаме тук, това ще бъде моментът Му.

Фиг. 4

За онагледяване на процеса на формиране на напреженията от огъващия момент Му, при анализа ще разглеждаме гредата не само с нейната ос (както се постъпва при намиране на разрезните усилия) а с пълното и напречно сечение (фиг.4). Освен това ще разглеждаме гредата не като непрекъсната среда, а като съставена от множество нишки, разположени успоредно на оста на гредата (·).

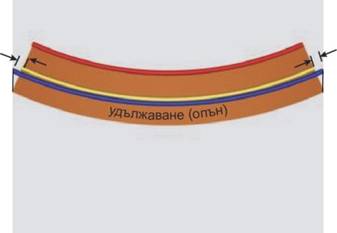
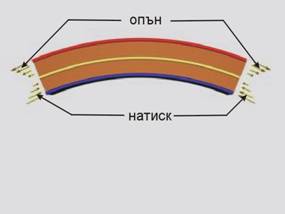
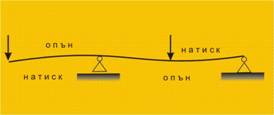
Когато върху гредата действа положителен момент, както е показано на фиг.4, тя се огъва така, че, както се вижда от фиг. 5, долните нишки са опънати (· ·), а горните са натиснати (фиг.6).

Фиг. 5 Фиг.6

Фиг.7 ·

Фиг.8

Фиг.9

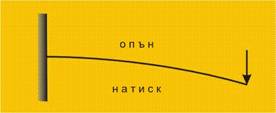
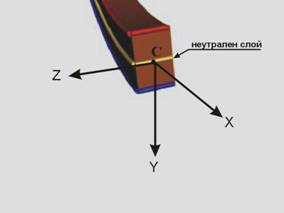
При това най-голям опън се реализира в нишките по долния ръб на гредата, а най-голям натиск - в горния ръб. Предполага се, че преминаването от опън към натиск става плавно, по линеен закон. Тогава между долния и горния ръб на гредата трябва да съществува нишка, която нито да е опъната, нито да е натисната. Тази нишка се нарича "неутрална". Доказва се, че такива нишки, които запазват първоначалната си дължина при огъване, съвпадат с центъра на тежестта на напречното сечение на гредата. Изобщо, ако се погледне напречното сечение, нишките, които се виждат по дължина, ще образуват хоризонтален слой. Поради това, по-коректно е да се говори не за неутрална нишка, а за неутрален слой (фиг.7).

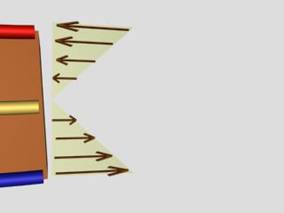
В напречното сечение на гредата, всяка нишка се вижда като точка, а усилията в нишките са аналогични на междучастичните сили, или на нормалните напрежения s. Тяхното разпределение е показано на фиг.8. В някои учебници диаграмата на натисковите напрежения се обръща (·), така че в окончателен вид, напреженията се представят с диаграми като тази на фиг.9. Условно се приема, че както и при разрезните усилия, положителните напрежения отговарят на опън, а отрицателните - на натиск.

Фиг. 10 ·

Както може да се предположи, отрицателният момент огъва гредата така, че опънатите нишки са отгоре, а отрицателните - отдолу · (фиг.10).

Изложеното до тук онагледява формирането на напреженията при чисто специално огъване, но не дава математичен апарат, с който те да бъдат изчислени, ако познаваме размерите на напречното сечение на гредата и големината на огъващия момент. Тук ще бъде показан извода на формула за изчисляване на нормалните напрежения при огъване на греда с правоъгълно напречно сечение.

Фиг.11

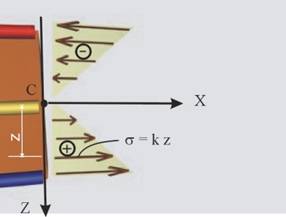
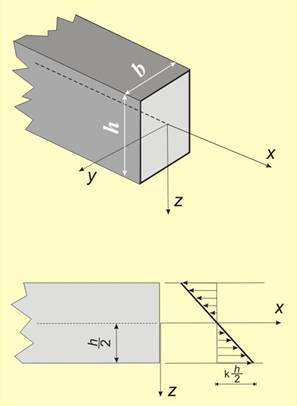
Според предпоставката за линейно разпределение, в точка, която се намира на разстояние z от неутралния слой, напрежението ще бъде

(уравнение на права линия).

С това уравнение нормалното напрежение лесно може да бъде определено, ако се познава коефициентът к. Той може да бъде определен, като се анализира формирането на огъващия момент М.

Фиг.12

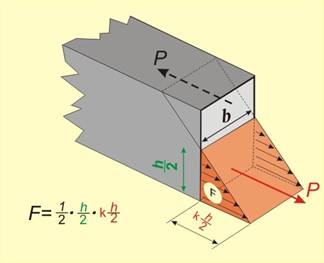
Нека да разгледаме греда, напречното сечение на която има височина h и ширина b (фиг. 12). В опънната зона максималната стойност на напрежението ще се получи при .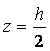

Фиг.13

Фиг. 14

Ако във всяка точка от сечението нанесем векторът-напрежение, ще се получи триъгълна призма (фиг.13) с обем

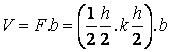. Този обем

определя големината на

силата, която действа в опънната зона на сечението. Или

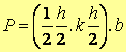
Силата в натисковата зона ще се получи със същата големина, но с обратна посока (фиг.14). Двете сили действат в центровете на тежестта на двете призми и образуват своица с рамо

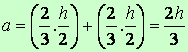(нека да напомним, че центърът на

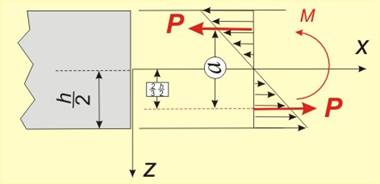
тежестта на правоъгълен триъгълник е на разстояние от острия ъгъл равно на 2/3 от дължината на катета, Ã). Моментът на тази двоица трябва да е равен на огъващия момент, или

М_у = Р.а = . =

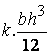
Изразът е инерционния момент I_y на сечението спрямо оста у, така че за момента се получава

M_у = k.I_y и .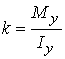

След заместване на получения израз за коефициента к в уравнението за напрежението , се получава израз, по който това напрежение лесно може да бъде определяно:

.

Фиг.15

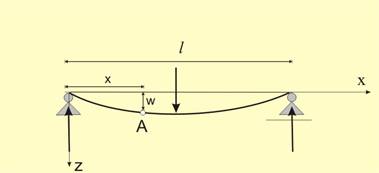
Освен напреженията, понякога е необходимо да бъдат определени и деформациите на огънатата греда. Следствие на приложените натоварвания, гредата загубва първоначалната си праволинейна форма (фиг.15). Новото очертание на оста на гредата (т.н. "еластична линия") обикновено се извежда математично (това ще бъде показано на лекциите) при предпоставката, че точките претърпяват само вертикални премествания w. Така, за да се познава еластичната линия, е необходимо да се познава как се изменя w с нарастване на х, или да се знае функцията w=f(x). Най-общо огъването следва правилото, че положителният огъващ момент опъва долни нишки.

За изпита най-малко трябва да се ориентирате в практическия подход, илюстриран със следните примери:

·

·

·

·