12. ОКРЪЖНОСТ НА НАПРЕЖЕНИЯТА ПРИ ДВУМЕРНО НАПРЕГНАТО СЪСТОЯНИЕ

Фиг.1

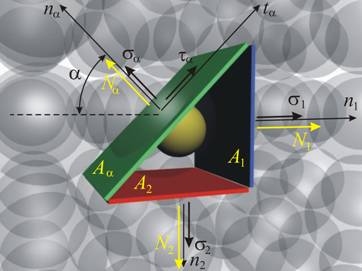
В предишен параграф беше показано, че при двумерно напрегнато състояние, ако са известни главните нормални напрежения, могат да бъдат определени напреженията във всяка друга площадка. За целта трябва да бъде даден ъгълът (a), който нормалата й сключва с една от осите (фиг.1). При анализ на равновесието на частицата, отделена от трите площадки, бяха изведени следните изрази за определяне на нормалното и тангенциалното напрежение:

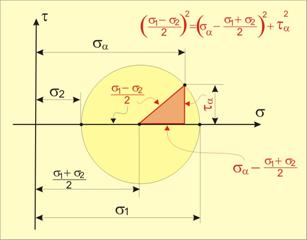
При преработка на двете уравнения (повдигане на квадрат и събиране на левите и десните страни за да се освободим от тригонометричните функции ·) се получава следният израз, свързващ нормалното и тангенциалното напрежение:

.

Фиг.2 ·

Полученото уравнение описва окръжност в координатна система sOt (фиг.2). Центърът на окръжността лежи на хоризонталната ос и е изместен от центъра на разтояние . Радиусът на окръжността е . Точките, които отговарят на напреженията в двете взаимно-перпендикулярни площадки (в случая – главните напрежения), лежат на диаметъра на окръжността. Този графо-аналитичен способ за представяне на напреженията в дадена частица е използван за първи път от Карл Кулман през 1866г., но е разработен по-късно подробно от Ото Мор (Otto Mohr), така че окръжността на напреженията е известна още и като “окръжност на Мор”.

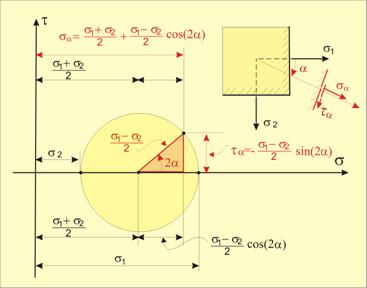
Може да се обобщи, че нормалното и тангенциалното напрежение във всяка площадка се изобразяват като точка от окръжност в ранината sOt. По-надолу ще бъде описано как тази окръжност може да бъде използвана при анализ на напрегнатото състояние в околността на частицата. Разгледани са две задачи, които условно са наречени права задача (дадени са главните напрежения, търсят се напреженията в произволна площадка) и обратна (дадени са напреженията в две произволни взаимно перпендикулярни площадки, търсят се главните напрежения).

Права задача Обратна задача