Права задача

Условие:

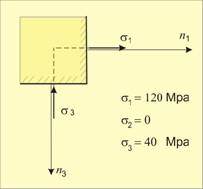
Дадени са главните напрежения при едно двумерно напрегнато състояние, изобразено на фиг.3. Да се определят напреженията в площадка, нормалата на която сключва с направлението на първо главно напрежение ъгъл a=-36^o.

Фиг. 3

Решение: (за аналитично решение – щракни тук)

1. Построяване на окръжността на Мор

Тъй като напреженията се измерват в паскали, а се изобразяват в координатната равнина с единици за дължина (в случая е подходящо това да става в сантиметри), преди да започне решението е необходимо да се въведе мащаб, с който да бъде определено един сантиметър от равнината на колко паскала отговаря.

Фиг.4

От фиг.3 се вижда, че разликата между напреженията (да обърнем внимание, че s₃ е на натиск, значи отрицателно) е 160 МРа. За да се разположи подходящо окръжността върху страницата с която разполагаме, тук ще бъде избран мащаб 1:20, или 1cm да отговаря на 20 МРа (фиг.4). Разделяме стойността на първо главно напрежение на мащаба: . Това е координатата по хоризонталната ос, по която нанасяме нормалните напрежения. Координатата по вертикалната ос ще бъде нула, тъй като в главните площадки няма тангенциални напрежения.

По такъв начин напрежението в първата главна площадка ще се изобрази от т.S₁ с координати (6, 0) ·. Напрежението във втората главна площадка ще се изобрази от т.S₃ с координати (-2, 0) ·. Центърът на окръжността е в средата между двете точки - т.О с координати (2, 0) ·. При известни център и диаметър, не представлява трудност да се построи и самата окръжност ·.

2. Определяне на напреженията в наклонената площадка

При графичното определяне на напреженията трябва да се има предвид следното:

Фиг. 5

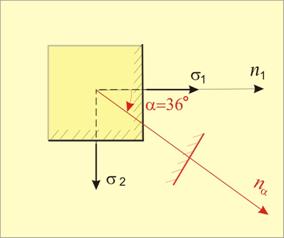
- При нанасяне на ъгъла a=-36^o, който наклонената площадката сключва с първа главна площадка, за положителна посока се приема посоката, обратна на часовниковата стрелка. Отрицателната посока е посоката на часовниковата стрелка. По такъв начин отрицателният ъгъл формира картината, показана на фиг.5 ·.

- Във формулата за определяне на тангенциалното напрежение в наклонената площадка участва синус на ъгъла (той е положителен за ъглите от 0 до 180^О) с отрицателен знак (когато ъгълът е положителен – тангенциалното напрежение е отрицателно). Поради това в окръжността отрицателните ъгли се нанасят в посока, обратна на часовниковата стрелка, за да формират положителни тангенциални напрежения ·. Положителните ъгли се нанасят в посока на часовниковата стрелка (отрицателни тангенциални напрежения).

- Във формулите за определяне на напреженията в наклонена площадка участва ъгълът 2a, който в окръжността се явява централен ъгъл (фиг. 2). При графичното построяване е удачно да бъде използван вътрешен ъгъл със същата дъга и връх в най-лявата точка на окръжността (за тази задача - т.S₃ ) ·.

Определянето на напреженията протича в следната последователност:

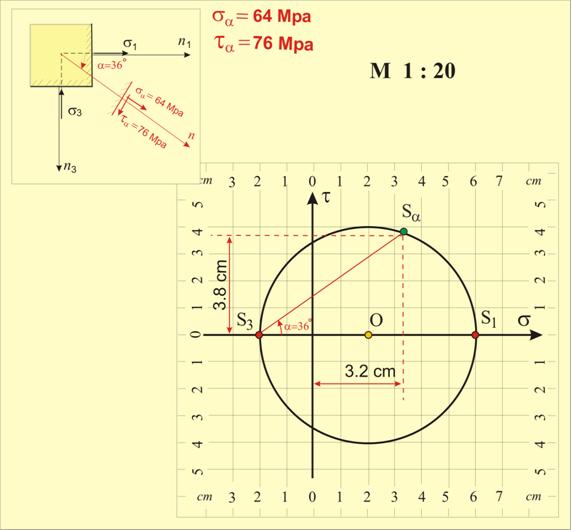
- През най-лявата точка на окръжността (т.S₃) се прекарва лъч, който е завъртян на ъгъл 36^o спрямо хоризонталната ос в посока, обратна на часовниковата стрелка (за отрицателен ъгъл). Пресечната точка на лъча с окръжността е т.S_a, която изобразява напреженията в завъртяната площадка (фиг. 6)·.

- Измерва се хоризонталната координата на т.S_a (3.2 cm). Измерената дължина се превръща чрез мащаба в напрежение (3.2 х 20 = 64 МРа). Полученото напрежение се записва като нормално напрежение s_a в завъртяната площадка ·. На схемата напрежението се изобразява насочено навън от площадката (положително напрежение).

- Измерва се вертикалната координата на т.S_a (3.8 cm). Измерената дължина се превръща чрез мащаба в напрежение (3.8 х 20 = 76 МРа). Полученото напрежение се записва като тангенциално напрежение t_a в завъртяната площадка ·.

На схемата напрежението се изобразява насочено така, че за да съвпадне по късия път положителната му посока с положителната посока на нормалата, да трябва да се завърти обратно на часовниковата стрелка (положително напрежение) ·.

Отрицателното напрежение се изобразява насочено така, че за да съвпадне по късия път положителната му посока с положителната посока на нормалата, да трябва да се завърти в посока на часовниковата стрелка ·.

С това задачата се смята за решена.