Главни напрежения

Фиг. 4

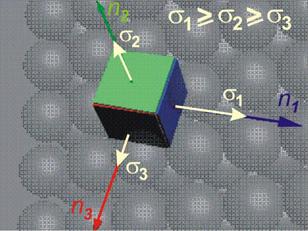
И така, да продължим с това, че при избор на различни тройки координатни оси, получаваме различни тензори на напреженията ·. При това, съществуват три площадки върху които тангенциалните напрежения са нула (върху тях действат само нормални напрежения ·). Такива площадки се наричат «главни площадки», а напреженията – «главни напрежения». Главните напрежения се номерират, като най-голямото е с номер 1 а най-малкото с номер 3 ·. Така се оформя картината, показана на фиг.4. В този случай, когато и трите главни напрежения са различни от нула, се казва че в околността на точката има тримерно напрегнато състояние.

Когато само две от главните напрежения са различни от нула се казва, че в околността на точката има двумерно напрегнато състояние. В този случай отпада необходимостта площадките да бъдат показвани в пространството и се преминава към равнинно изобразяване. Това става като престанем да се интересуваме от тази площадка, върху която няма нормално напрежение · и завъртим останалите две площадки така, че да гледаме срещу нормалата на първата ·. Така всяка площадка се изобразява с отсечка, като от страна на материалната частица областта се щрихова.

Фиг. 5

Фиг. 6

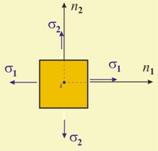
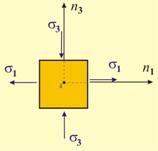
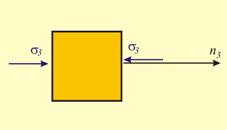
На фиг. 5 са представени три случая на двумерно напрегнато състояние според подредбата на нормалните напрежения (s₁ ≥ s₂ ≥ s₃) и тяхната големина. При това се отчита, че когато напрежението действа навън от площадката, частицата е натоварена на опън и напрежението е положително. Когато напрежението действа навътре към площадката, частицата е натоварена на натиск и напрежението е отрицателно.

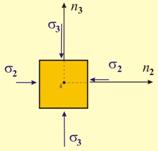
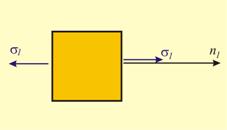
Когато само едно от главните напрежения е различно от нула, напрегнатото състояние е едномерно. При него са възможни два случая, в зависимост от това, дали частицата е натоварена на опън или на натиск (фиг.6).

По-нататък при отделните теми изложението ще бъде съсредоточено върху двумерното напрегнато състояние.

Продължение: Аналитично изследване на двумерно напрегнато състояние >>>>>