Аналитично изследване на двумерно напрегнато състояние

Фиг.7

Фиг. 8

Фиг. 9

Фиг. 10

В началото на темата беше казано, че за да познаваме напрегнатото състояние в околността на точка (частичка) е достатъчно да познаваме напреженията в три взаимно перпендикулярни площадки, а за двумерно напрегнато състояние – напреженията в две взаимно перпендикулярни площадки.

Тук това ще бъде доказано за двумерно напрегнато състояние с решаването на следната задача:

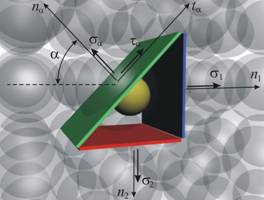
Дадено: Известни са главните нормални напрежения (s₁, s₂) и площадка, определена с ъгъла a, който нормалата на площадката сключва с нормалата n₁ на първата главна площадка · (фиг. 7).

Търси се: Нормалното напрежение s_a и тангенциалното напрежение t_a в площадката.

Решение:

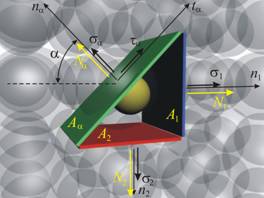
Решението на задачата се извежда от условията за локално равновесие на частичката, записани спрямо двете основни направления, свързани с прощадката – нормалното n и тангенциалното t. Действащите сили са (фиг. 8): N₁ върху площадката с нормала n₁,

N₂ върху площадката с нормала n₂,

Na върху площадката с нормала n_a,

Тa върху площадката с нормала n_a, но по направление на t_a.

Преди да се премине към записване на условията за равновесие е необходима малка предварителна подготовка, при която да се определи големината на действащите сили:

Големината на тези сили може да се получи по схемата “напрежение по площ“ (фиг. 8):

(a)

Площите А₁, А₂ и А_a на площадките не са независими, тъй като са страни в един правоъгълен триъгълник, и между тях съществуват тригонометричните зависимости

, от където , и , от където .

Като се заместят изразите за А₁ и А₂ в уравненията (a), тази връзка се прехвърля и върху силите:

(b)

Сега може да си премине към записване на условията за равновесие.

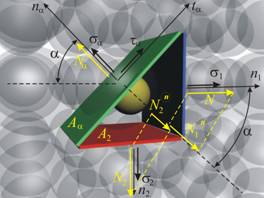
Първото условие е, че сумата от проекциите на силите, действащи по направление на n_a трябва да е нула (фиг. 9):

или . (c)

Големината на проекциите е ·:

и .

След като тези стойности се заместят в равенството (c), то добива вида:

Следващата стъпка е силите N₁, N₂ и N_a да бъдат заместени по ур. (b):

.

В полученото уравнение

може да се съкрати членът А_a , s_a да се остави в ляво, а останалите членове да се прехвърлят в дясно. Така се получава изразът, по който се определя нормалното напрежение:

. (d)

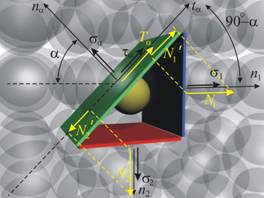
Второто условие е, че сумата от проекциите на силите, действащи по направление на t_a трябва да е нула (фиг. 10):

или . (е)

Големината на проекциите е ·:

и .

След като тези стойности се заместят в равенството (е), то добива вида:

Следващата стъпка е силите N₁, N₂ и T_a да бъдат заместени по ур. (b):

.

В полученото уравнение

може да се съкрати членът А_a , t_a да се остави в ляво, а останалите членове да се прехвърлят в дясно. Така се получава изразът, по който се определя тангенциалното напрежение:

. (f)

И така, ако са известни напреженията s₁ , s₂ и ъгълът a, по уравнения (d) и (f) могат да бъдат определени напреженията s_a и t_a .

С това задачата се смята за решена.