11. Напрегнато състояние в околността на точка (частичка). Главни напрежения. Аналитично изследване на двумерно напрегнато състояние

Фиг. 1

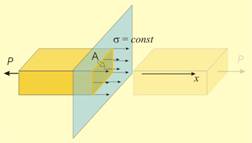
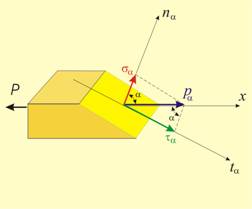
В предишен материал беше показано, че при опън и натиск напреженията освен от местоположението на разглежданата точка зависят и от направлението на равнината (площадката) по която се анализира междучастичното взаимодействие (фиг.1):

,

.

Този извод може да се разшири и за други направления в пространството. Съвкупността от напреженията в дадена точка, отговарящи на всички възможни площадки, се нарича напрегнато състояние.

Така задачата за определяне на напреженията става на пръв поглед неопределена, тъй като през една точка могат да бъдат прекарани безброй много направления, на които отговарят безброй много площадки и неизвестни напрежения ·.

На практика се оказва, че е достатъчно да се познават напреженията само в три взаимно перпендикулярни площадки около частицата, за да се познава напрегнатото състояние. Това ще бъде доказано малко по-нататък в този материал, а тук ще бъде продължено с напреженията върху трите площадки, които описват напрегнатото състояние.

Нека трите направления определящи площадките са направленията на трите координатни оси Ох ·, Оу · и Oz ·. Във всяка от площадките напрежението се представя с двете си компоненти – нормално напрежение s и тангенциално напрежение t. В общия случай тангенциалното напрежение има произволно направление в площадката и трябва да бъде разложено по направленията на координатните оси ·.

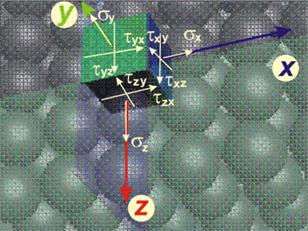
Фиг. 2

За да се отличават едно от друго, напреженията носят индекс, който съвпада с името на нормалата · (оста, перпендикулярна на площадката). Така обаче във всяка площадка се получават две тангенциални напрежения с еднакъв индекс. За да се отличават тангенциалните напрежения в една площадка, към името им се прибавя втори индекс, показващ направлението, по което са насочени. Така например, в площадката с нормала оста Ох · освен нормалното напрежение s_x ще се получат тангенциалните напрежения t_xy (лежащо в площадка с нормала х и насочено по направление на оста у) и t_xz (лежащо в площадка с нормала у и насочено по направление на оста х). Същото важи и за площадките с нормали Оy и Оz ·. Така окончателно се оформя картината, показана на фиг.2.

За дадена точка напрегнатото състояние може да се определи с кои да е три взаимно перпендикулярни площадки. При аналитично изследване на напрегнатото състояние често се прилага матрично смятане, поради което напреженията в площадките се подреждат в матрица:

Елементите на тази матрица не са произволни. При избор на друга тройка оси, напреженията в новите площадки могат да бъдат получени от напреженията в старите площадки, трансформирани с ъглите между старите и новите оси. Матрици с такава зависимост между елементите при смяна на координатната система се наричат «тензори». Поради това по-нататък ще се говори за «тензор на напреженията» и съответно «тензор на деформациите».

В тензора на напреженията трите колони отговарят на напреженията в трите площадки, а трите реда - на напреженията по трите направления.

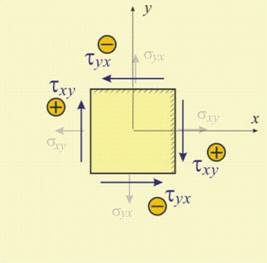
Фиг. 3

Може да бъде доказано, че за тензора на напреженията важи правило за съответствие на тангенциалните напрежения във взаимно перпендикулярните площадки. Според това правило напреженията в две взаимно перпендикулярни площадки са равни по големина:

t_xy = t_yx ; t_xz = t_zx ; t_yz = t_zy ,

и противоположни по знак · (фиг.3). Това означава, че ако в едната площадка напрежението (например t_xy) е насочено към общия ръб, то и в другата площадка напрежението (съответно t_yx) трябва да е насочено към него ·. Ако в едната площадка напрежението “бяга” от общия ръб, то и в другата площадка напрежението трябва “бяга” от ръба.

Продължение: Главни напрежения >>>>>