38.
Bалове и оси. Якостно
пресмятане. Критична ъглова скорост на валове.
|
МАТЕРИАЛИТЕ В ТОЗИ РАЗДЕЛ СА ПОДГОТВЕНИ С
ПОМОЩТА НА ГЕРГАНА ИВАНОВА
(ЕК 282) ОТ КРЪЖОКА ПО ТЕХНИЧЕСКА МЕХАНИКА |
МАТЕРИАЛЪТ Е УЧЕБЕН И НЕ МОЖЕ ДА БЪДЕ
ИЗПОЛЗВАН ЗА
ПРЯКА КОНСТРУКТОРСКА ДЕЙНОСТ
|
|
Според
“Физико-математическа и техническа енциклопедия, БАН, 2000”, осите и валовете
са машинни елементи, обикновено с цилиндрична форма, с постоянно или променливо
напречно сечение, върху които са закрепени въртящи се или осцилиращи машинни
елементи. Осите и валовете си приличат по външен вид и могат да бъдат раличени
помежду си само по функциите, които изпълняват.
Осите служат само да
поддържат машинни елементи които се въртят или осцилират. Могат да бъдат
разглеждани като греди с кръгло напречно сечение, подложени на опън (натиск), срязване и огъване.
Валовете
са предназначени основно да предават въртящ момент от една машинна част на друга. Поради това тяхното основно
натоварване е на усукване. Освен усукване, външните сили пораждат във
валовете и огъващи моменти. Когато е необходимо, тези огъващи моменти се
включват в изчислителната процедура наред с усукващите.
Огъване при валовете обаче
се предизвиква не само от външните сили. Понякога закрепените върху вала части (ремъчни
колела, ротори на електромотори и турбини) не са добре
балансирани и центърът на тежестта им не лежи върху геометричната ос, около
която се върти вала. Това паражда инерционни (центробежни сили),
насочени перпендикулярно на оста на вала, които го огъват. При бавно въртящите
се части инерционните сили могат да бъдат пренебрегнати. При бързо въртящите се
валове инерционните сили немогат да бъдат пренебрегнати и трябва да бъдат взети
под внимание.
|
Фиг.1 |
По-нататък в изложението е показан подходът за
определяне на условията, при които работят бързооборотните валове, така, както
са изложени в «Д.ДИМИТРОВА,
Г.ГЕНОВ, ПРИЛОЖНА МЕХАНИКА, ВХТИ-БУРГАС, 1984Г.»
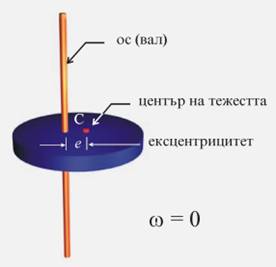
На фиг. 1a е показан
схематично диск на активна турбина или центрофуга с маса m, закрепен върху
достатъчно гъвкав вал. Масата на вала в сравнение с масата на диска е много
малка и за опростяване на разглаждането може да бъде пренебрегната. Центърът на
масата на диска не съвпада с оста на въртене на вала, а е изместен от нея на
разстояние е, което се нарича ексцентритет. При въртене на вала
центърът на масата ще се движи по окръжност с радиус r и върху вала
ще започне да действа центробежна сила Рс
·, формирана от масата т и нормалното
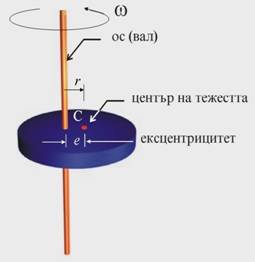
ускорение ап. В началото на въртенето радиусът е равен на
ексцентрицитета (r=e, фиг.1b) и центробежната сила е:
![]() (1)
(1)
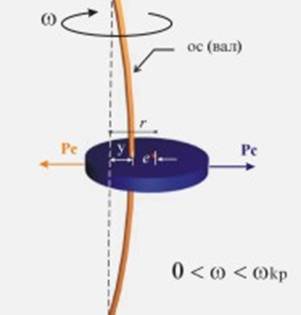
Под действие на тази
сила валът ще получи присвиване y, в резултат на което
центърът на масата на диска ще се върти по окръжност с радиус r=y+e (фиг.2).
Действителната центробежна сила ще стане по-голяма и ще се определи по израза
|
Фиг.2 |
![]() .
.
Тази сила се
уравновесява от силата на еластичност Ре
на вала, която е пропорционална на провисването у:
Ре = к у,
където к е силата,
която предизвиква единица провисване.
При дадена ъглова
скорост еластичната сила уравновесява центробежната:
Рс = Ре
или m(y+e)w2 = k y. (2)
Решено спрямо у, уравнение (2)
става:
![]() ®
®![]() ®
®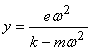 и
и 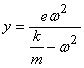 .
.
Ако означим
![]()
динамичното провисване
у на вала ще се запише чрез израза
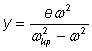 (3)
(3)
|
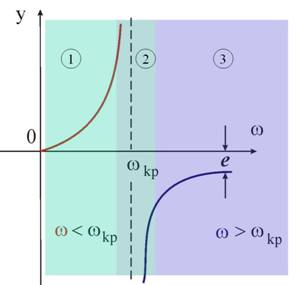
Фиг. 3 |
За всеки вал, със
закрепените върху него части, като система с определена еластична
характеристика, критичната ъглова скорост има някакво постоянно значение wkp=const. На тази основа можем да проследим изменението
на динамичното провисване на вала в зависимост от изменението на ъгловата
скорост (фиг.3).
-
Област
При w=0,
у=0. С
увеличаване на w числителят
нараства, а знаменателят намалява, т.е. динамичното провисване у нараства ·.
-
Област ‚
Когато w=wkp динамичното
провисване става безкрайно голяма величина (на
практика това води до разрушаване на вала ·).
-
Област ƒ
При ъглова скорост
по-голяма от критичната ъглова скорост, у отново получава определено, но
отрицателно значение и при w®∞ у® -е. Това явление се нарича самоцентриране на системата, т.е.
центърът на масата на диска съвпада с оста на въртене. В това положение той
остава неподвижен, а огънатият на размер е (равен на
ексцентритета) вал се върти около вертикална осова линия, която минава през
центъра на масата на диска ·.
Турбината не може да
работи при ъглова скорост на въртене близка до wkp, тъй като при това
настъпва опасно увеличаване на у и на напреженията в тялото на вала. Центобежната сила на
диска натоварва опорите на системата със знакопроменливи вертикални и
хоризонтални натоварвания, които предизвикват вибрация на фундамента.
Ако валът се разположи
хоризонтално, то от действието на силата на тежестта той ще получи провисване у0, т.е. G=ky или mg=ky.
За критичната ъглова
скорост, след заместване на величините k и m в (2) и
преобразуване се получава
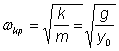 (4)
(4)
От уравнение (14) се
вижда, че критичната ъглова скорост не зависи от е, т.е.
системата ще има критична ъглова скорост и когато дискът е идеално балансиран. За
удобство върху основата на (4) и известия израз ![]() се изразяват критичните обороти на вала:
се изразяват критичните обороти на вала:
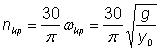 (5)
(5)
От анализа на (3) се
изясни, че валовете могат да работят със скорости по-малки от критичната и със
скорости по-големи от критичната. За да не се допусне развитие на явлението резонанс,
преминаването през зоната на критичната скорост трябва да стане с достатъчна
бързина.
Валовете, които работят
при скорости по-малки от критичните се наричат корави валове. За тях n≤(0,7÷0,8)nkp. Валовете,
които работят при скорости по-големи от критичните се наричат еластични. За тях
n=(1.4÷2.0)nkp.