ТЕОРЕМА ЗА КИНЕТИЧНАТА ЕНЕРГИЯ НА МЕХАНИЧНА СИСТЕМА

В предишна тема беше формулирана теорема за кинетичната енергия на материална точка, която гласи: "диференциалът на кинетичната енергия на движеща се точка е равен на елементарната работа на действуващата върху точката сила" и се изразява със следното уравнение:

Тази теорема може да се обобщи за система от п на брой материални точки. При нея ще се получи система от п на брой такива уравнения - за всяка i^та точка по едно:

.

Като се сумират левите и десните страни на уравненията от тази система, се получава:

и .

В лявата страна на това равенство, е кинетичнатаенергия на системата. Така се получава:

.

Това уравнение изразява в диференциална форма теоремата за кинетичната енергия на механична система, която гласи: "диференциалът на кинетичната енергия на механична система е равен на сумата от елементарната работа на действуващите върху точката външни и вътрешни сили".

В техническите задачи често механичните процеси се разглеждат в даден период от време между два момента - нулев t₀ (начален) и краен t₁. Интегрирането на уравнението от закона между тези два момента може да се проведе в следната последователност:

® ® ®

или: "промяната на кинетичната енергия на системата е равна на пълната работа на приложените сили".

Всеки инженер, който реши да използва уравнението от тази теорема при решаване на конкретни проблеми, трябва да умее да определя кинетичната енергия на телата, съставящи системата, за да формира лявата част на равенството, и да определя работата на сили, действащи върху системата, за да формира дясната част на равенството. В някои случаи това може да се окаже не толкова лесна задача, тъй като телата от механичните системи понякога извършват сложни движения. За най-често срещаните в техниката движения (транслационно, ротационно и равнинно), приложението на теоремата ще бъде илюстрирано със следния пример:

Фиг.1

Фиг.2

Фиг.3

Фиг.4

Фиг.5

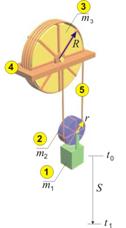
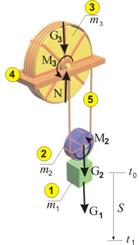
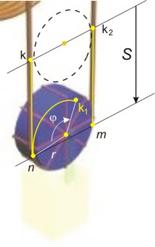
Механична система от три тела с известни маси и размери (фиг.1) преминава в момента t₀ от покой в движение ·, при което тялото  се движи транслационно вертикално надолу и до момента t₁ изминава път S. Тялото ‚ представлява диск, оста на който е свързана с тяло  така че се движи заедно с него. През диска е прехвърлена гъвкава неразтеглива нишка …, единият край на която е закрепен върху неподвижна платформа „, а другият край е навит около диска ƒ. По време на движението нямя приплъзване между нишката и дисковете. Оста на диска ƒ също е закрепена върху неподвижната платформа. Осите на двата диска са лагерувани, което позволява свободното им въртене по време на движението.

Илюстрацията ще се състои във формиране за тази система на уравнението от теоремата за кинетичната енергия.

Тъй като телата са три, членовете на уравнението ще носят долни индекси от 1 до 3, които ще показват за кое тяло се отнасят, и горни индекси, които ще означават момента, за който се отнасят ( " ⁽⁰⁾ " за t=t₀ и " ⁽¹⁾ " за t=t₁). Така уравнението на теоремата става

1. Лява част на уравнението - кинетични енергии

Системата се състои от три тела, които ще бъдат разгледани по отделно.

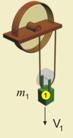
- Тяло  ·(фиг.2).

Тъй като това тяло извършва транслационно движение и всички точки имат еднакви скорости, кинетичната му енергия се определя както при материална точка:

,

където V₁ е скоростта на масовия център на тялото.

Тялото ‚ има най-сложно движение, така че ще бъде разгледано последно.

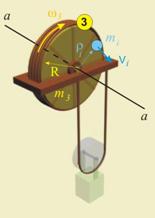
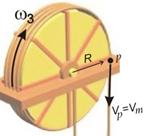
- Тяло ƒ ·.

Това тяло представлява диск, който се върти около неподвижна ос (ротационно движение). За осите като конструктивен елемент е предвидена специална тема, така че за сега тази ос ще бъде приета за линия а-а, около която се върти диска (фиг.3).

Ако разгледаме една точка (i) от диска, отстояща на разтояние r, то скоростта на тази точка ще бъде V=wR, а кинетичната енергия:

.

Кинетичната енергия на тялото ще бъде сумата от кинетичната енергия на всичките му точки:

.

Сумата е масовия инерционен момент на тялото. Така окончателно, за кинетичната енергия на тялото се получава:

.

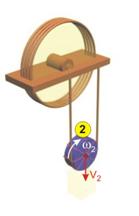
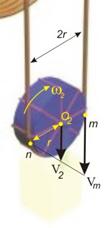
- Тяло ‚ ·

Това тяло е диск, който извършва най-сложното движение от телата в системата. От една страна, оста на диска е свързана с тялото  и се движи заедно с него вертикално надолу със скорост V₂ (фиг.4). От друга страна, нишката, която е прехвърлена през диска, го свързва с тялото ƒ и предизвиква завъртане с ъглова скорост w₂. Такова движение, което може да се разглежда като съвкупност от две движения - преместване (транслационно движение) и завъртане (ротационно движение) вече беше разгледано в темата за равнинно движение. При това движение кинетичната енергия може да бъде получена като сума от кинетичните енергии на двете движения:

,

където V₂ е скоростта на масовия център на тялото (центъра на диска).

С това нещата в лявата страна на равенството са изяснени и може да се премине към дясната страна на равенството, която съдържа работите А_i на силите, действащи върху системата.

Като се пренебрегне теглото на нишката, върху системата остават да действат шест сили и моменти (силите на тежестта G₁, G₂ и G₃, реакцията на платформата N и моментите на триенето в лагерите М₂ и М₃, фиг.5), които ще бъдат разгледани по отделно.

- Сили на тежестта на първото тяло G₁, и на второто тяло G₂

При тези сили работата се определя лесно, тъй като направлението посоката на силите съвпада с направлението и посоката на преместването:

AG₁ = G₁.S ; AG₂ = G₂.S

- От условието оста на третото тяло да е неподвижна следва, че силата на тежестта на второто тяло G₂ и реакцията на платформата N се уравновесяват. Освен това, когато приложната точка няма преместване, силата не извършва работа. Следователно, AG₃ = 0 ; A_N = 0.

Фиг.6

Фиг.7

Фиг.8

Фиг.9

- Моменти на триенето М₂ и М₃.

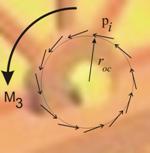
В зависимост от начина на лагеруване, при осите на двата диска се получават моменти на триене, съпротивляващи се на движението и насочени обратно на посоката на ъгловата скорост (фиг.6 за третото тяло). Тези моменти се пораждат от сили на триене в точките по околната повърхност на оста, където тя контактува с диска. Например, ако радиусът на оста на третото тяло е r_oc (фиг.7) и силата на триене в една i^та точка е р_i , моментът на тази сила ще бъде М_i=р_ir_oc . Пълният момент на триене ще бъде .

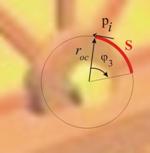
Ако дискът се завърти на ъгъл j₃ , приложната точка на силата р_i ще измине път S, равен на дължината на дъгата на централен ъгъл j₃ в окръжност с радиус r_oc. От геометрията се знае, че S=j₃r_oc (фиг.8). Тогава извършената работа ще бъде . Работата е отрицателна, тъй като преместването е в посока, обратна на посоката на силата. Пълната работа ще бъде , и понеже , се получава:

.

Аналогично, за момента на триене в оста на второто тяло може да бъде записано:

.

Тъй като по условие е дадено преместването S, за окончателното определяне на работата е необходимо двата ъгъла на завъртане j₂ и j₃ да бъдат изразени через това преместване. Например, ако разгледаме два момента от движението на второто тяло · (фиг.9), ще видим, че за да се придвижи центърът на диска вертикално надолу на разтояние S, той трябва да измине път (да се претъркаля) по нишката с държина . От условието да няма преплъзване между нишката и диска следва, че дъгата на ъгъла на завъртане ще бъде равна на изминатия път - . От геометрията се знае, че централният ъгъл на тази дъга е , от където:

, или също .

От фиг.9 се вижда също, че за да се извърши движението, нишката трябва да се удължи с

От условието че нишката е неразтеглива следва, че това удължение може да се реализира само через развиване на нишка от третото тяло через завъртането му на ъгъл j₃ . Като се вземе предвид, че дъгата на този ъгъл трябва да бъде 2S, а радиусът на диска е R, се получава:

.

Така, за дясната страна на уравнението се получава:

SA_i = AG₁ + AG₂ + AG₃ +A_N + + = G₁.S + G₂.S + 0

и SA_i = ( G₁+ G₂) S

Сега да се върнем към уравнението на теоремата:

® (E₁+E₂+E₃ )⁽¹⁾ - (E₁+E₂+E₃ )⁽⁰⁾ = ( G₁+ G₂) S

В началния момент тялото е в покой, така че скоростите на телата са нула. От това следва:

E₁⁽⁰⁾ = ,

E₂⁽⁰⁾ = ,

E₃⁽⁰⁾ = ,

или (E₁+E₂+E₃ )⁽⁰⁾ = 0+0+0= 0

Така уравнението добива вида: (E₁+E₂+E₃ )⁽¹⁾ - 0 = ( G₁+ G₂) S

Като заместим получените изрази за кинетичната енергия и работата, и като пропуснем горния индекс, тъй като е ясно, че параметрите в уравнението важат за крайния момент на движението, уравнението се получава:

++ = ( G₁+ G₂) S

В различните задачи всеки един (но само един) от параметрите, участващ в уравнението, може да бъде разглеждан като неизвестен. Нека да разгледаме случай, в който зa поставения пример се търси скоростта на първото тяло в края на движението при известни сили, или V₁⁽¹⁾=?. Тъй като освен тази скорост, неизвестни се явяват и останалите скорости, на пръв поглед задачата е нерешима, тъй като се разполага с едно уравнение за тяхното определяне. Телата обаче образуват механична система, което означава, че движението им е взаимно-обвързано. Това може да се използва, за да се изразят всички скорости само через тази, която се търси. Тъй като в случая това е скоростта на първото тяло, за целта ще бъде разгледано движението на останалите тела.

Фиг.10

Тялото ‚ е свързано с първото тяло така, че по време на движението центърът на диска има същата скорост като него,

или V₂=Vo₂=V₁ (Фиг.10).

От друга страна, скоростта на центъра на диска може да бъде определена като скорост на точка от тяло, извършващо равнинно движение с моментен център на въртене в т.п:

.

Тъй като левите страни на двете уравнения са равни (и двете съдържат само V₂), то и десните страни трябва да бъдат равни: , от където се получава:

.

Фиг.11

Моментният цeнтър на скоростите в този случай се определя по следната логика: Левият клон на нишката е неподвижно свързан с платформата, поради което всички точки от този клон са неподвижни, включително и т.п, в която диска контактува с нишката. Тъй като по условие няма приплъзване между диска и нишката, тази точка може да бъде разглеждана и като неподвижна точка от диска, което значи че е моментен център на въртене.

Второто и третото тяло са свързани посредством десния клон на нишката. Тъй като нишката е неразтеглива, всички точки от нея ще имат еднакви скорости. Скоростта на т.т може да бъде определена като скорост на точка от тяло (фиг.10), извършващо равнинно движение с моментен център на въртене в т.п (няма приплъзване между нишката и тялото):

или

Същият клон на нишката контактува с третото тяло в т.р (фиг.11). От една страна, скоростта на тази точка може да бъде определена като на точка от нишката:

Vp = Vm,

а от друга - като скорост на точка от тяло, извършващо ротационно движение с ъглова скорост w₃:

.

Тъй като левите страни на двете уравнения са равни (и двете съдържат само V_p), то и десните страни трябва да бъдат равни: , от където се получава:

или .

Като се заместят получените връзки между скоростите, уравнението на теоремата добива вида:

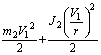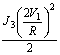++ = ( G₁+ G₂) S ,

V₁² ( ++ ) = 2 ( G₁+ G₂) S

и 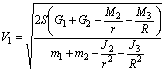.