РАБОТА И МОЩНОСТ. ТЕОРЕМА ЗА КИНЕТИЧНАТА ЕНЕРГИЯ НА ТОЧКА.

· ТЕОРЕМА ЗА КИНЕТИЧНАТА ЕНЕРГИЯ

Кинетична енергия на една точка с маса т и скорост v наричаме скаларната величина Е, определена от израза

(9)

Ще докажем следната теорема, за кинетичната енергия: ДИФЕРЕНЦИАЛЪТ НА КИНЕТИЧНАТА ЕНЕРГИЯ НА ДВИЖЕЩА СЕ ТОЧКА Е РАВЕН НА ЕЛЕМЕНТАРНАТА РАБОТА НА ДЕЙСТВУВАЩАТА ВЪРХУ ТОЧКАТА СИЛА.

Изхождаме от основното уравнение на динамиката

m a = P ( т- маса, 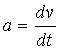- ускорение, Р- сила),

двете страни на което умножаваме скаларно със скоростта v :

m v = P v , от където се получава m v dv = P v dt . (10)

При анализа на получения израз трябва да се има предвид че:

1. d(v²) = 2 v dv, от където следва и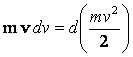

2. , от където P v dt = ( dA е елементарната работа на силата Р)

Като се заместят тези два израза в уравнение (10), се получава диференциалната форма на теоремата:

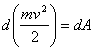(11)

Като интегрираме тази форма за периода на движение между началната т.1 и крайната т.2 , се получава интегралната форма на теоремата:

, или

( v₁- скорост в началната точка 1, v₂- скорост в крайната точка 2, А₁₂ - пълната работа, извършена от силата при преместване от т.1 в т.2)

т.е. ИЗМЕНЕНИЕТО НА КИНЕТИЧНАТА ЕНЕРГИЯ НА ТОЧКА Е РАВНО НА ПЪЛНАТА РАБОТА НА СИЛАТА, ДЕЙСТВАЩА ВЪРХУ НЕЯ.

ПРОДЪЛЖИ >>>