РАБОТА И МОЩНОСТ. ТЕОРЕМА ЗА КИНЕТИЧНАТА ЕНЕРГИЯ НА ТОЧКА.

· Работа на еластична сила.

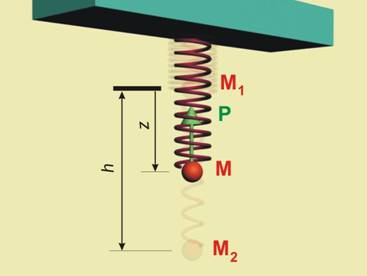
Фиг. 1

Нека имаме пружина, на която (фиг. 1) единият край е неподвижно хванат, а другият е свободен. Точка М₁ съответствува на положението, което заема свободният край при положение на равновесие на пружината. Ако опънем пружината, в нея се появява еластична сила Р, чиято големина е пропорционална на деформацията на пружината, направлението й е по оста на пружината, а посоката — обратна на оста z, определяща положението на свободния край спрямо началното му положение М₁. Следователно Р = - сz. Коефициентът с се нарича пружинна константа и има измерение N/m.

Елементарната работа на силата Р съгласно уравнение 2 ще бъде dA = P dz = -c z dz.

Пълната работа при опъване на пружината и придвижване на свободния край от т.М₁ до т.М₂ ще бъде

(6)

където h представлява деформацията на пружината. В случай, когато пружината се свива след удължаване за да добие първоначалния си размер, > 0.

Както се вижда от израза (6) еластичната сила е също една потенциална сила.

Когато движението е отклоняване от равновесното положение, еластичната сила е насочена винаги обратно на посоката на движението и извършваната работа е отрицателна, независимо дали се извършва удължаване · на пружината или скъсяване ·.

Ако движението е възтановяване на равновесното положение, посоката на еластичната сила съвпада с посоката на движението · и извършваната работа е положителна.

ПРОДЪЛЖИ >>>