РАБОТА И МОЩНОСТ. ТЕОРЕМА ЗА КИНЕТИЧНАТА ЕНЕРГИЯ НА
ТОЧКА.
·
РАБОТА
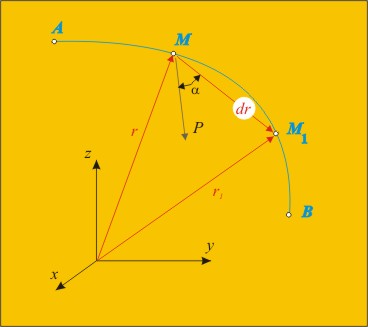
Нека М и M1 да бъдат две
безкрайно близки положения (фиг.1) на движещата се точка М под действие на
силата Р. Известно е, че елементарното преместване на точката ще бъде dr. Елементарна работа dA на
силата Р се нарича скаларното произведението от вектора-сила P и вектора-елементарно преместване dr:
dA
= P dr (1)
|
Фиг.1
Фиг.2 |
Големината на елементарната работа е стойността на
скаларното произведение – dA=P.dr.cosa. . Според
този израз работата е равна на произведението от преместването и проекцията на
силата върху направлението на преместването. Така една сила не извършва работа,
ако направлението и е перпендикулярно на силата.
Дясната част на уравнение (1) представлява скаларно
произведение на два вектора.
Ако векторът dr е перпендикулярен на Р,тогава dА=0.
Ако проекциите на Р върху осите на
координатната система Охуz са Рх, Рy, Рz , а
тези на dr са съответно dx, dy, dz,
dA = Px dx + Py dy + Pz dz
(2)
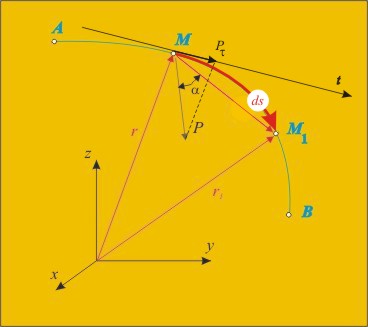
Ако законът на движение е
зададен в естествена форма (фиг.2), то работата се определя с криволинейната
координата ds и проекцията на силата Р върху тангентата към траекторията, или
dA = Pt ds (3)
Уравненията (1), (2), (3)
съответствуват на трите начина на задаване на движението — векторен,
координатен и естествен.
Равнодействащата
на една сходяща система сили е
R
= P1 + P2 …+Pi …+Pn
и
преместването за всички сили от системата е едно и също - dr. Kато заместим този израз в уравнение (1),
получаваме:
R dr= P1 dr+ P2
dr +…+Pi dr +…+Pn dr ,
dA = dA1+ dA2
+…+ dAi +…+ dAn ,
или елементарната работа на отделните сили на една сходяща система сили е равна
на елементарната работа на равнодействащата на системата.
Ако трябва да намерим
работата, която извършва силата за едно крайно преместване, например от точка А
до В (фиг. 1), е необходимо да интегрираме уравнения (1), (2) или
(3). Криволинейният интеграл (ако такъв съществува) се нарича пълна работа:
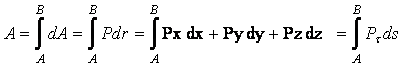 (4)
(4)
Работата
се измерва в джаули. Един джаул е работата, която извършва сила
1 нютон при преместване по
направление на силата, равно на един метър,
т. е. 1 J = 1 Nm.