РАБОТА И МОЩНОСТ. ТЕОРЕМА ЗА КИНЕТИЧНАТА ЕНЕРГИЯ НА ТОЧКА.

r ЗАДАЧА №1

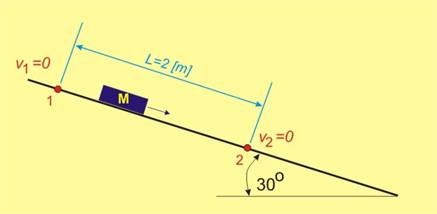
Фиг. 1

УСЛОВИЕ:

Тяло М с маса т се спуска без начална скорост по наклонена равнина (фиг.1). Коефициентът на триене между равнината и тялото е m=0.1.

Да се определи скоростта на точката в момента, когато е изминала път L от два метра.

РЕШЕНИЕ:

Моментът на тръгване ще определим като първи, и характеристиките на движението в този момент ще носят индекс (1). Моментът в който точката е изминала първите два метра ще определим като втори, и характеристиките на движението в този момент ще носят индекс (2).

Тялото извършва транслационно движение, всички точки от него имат равни скорости и ускорения и за анализ на движението може да бъде прилаган апаратът от динамика на точка.

За решаване на задачата ще използваме теоремата за кинетичната енергия в нейния интегриран вид:

,

или разликата между кинетичната енергия във втория момент Ек₂ и кинетичната енергия в първия момент Ек₁ е равна на работата А₁₂, извършена от силите, действащи върху точката.

Очевидно, за да решим задачата, трябва да определим трите члена Ек₂, Ек₁ и А₁₂, участващи в равенството.

За кинетичната енергия имаме израза 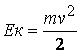, така че за първите два члена се получава:

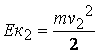и 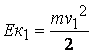(v е скоростта на точката).

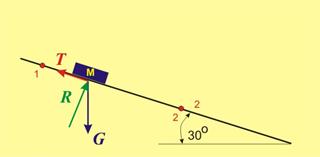
Фиг.2

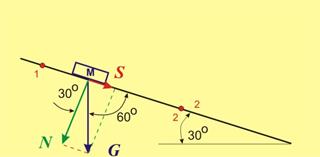
Фиг.3

По време на движението върху точката действат три сили - силата на тежестта G, реакцията на равнината R и силата на триене Т (фиг.2). Така, работата А₁₂ се получава като сума от следните три събираеми:

- Работа на силата на тежестта A_G

По определение работата Ар на една сила Р при преместване на приложната й точка на разстояние L е Ар=РLcos(a), където a е ъгълът между силата и преместването (и двете се изобразяват като насочени отсечки, така че при определяне на ъгъла трябва да се внимава за посоките им).

Силата на тежестта можем да разложим на две компоненти - едната по направление на движението (успоредно на равнината) S и другата - нормална на равнината N (фиг.3).

Посоката на S съвпада с посоката на преместването, което означава, че работата на силата на тежестта е бъде положителна. От фигурата се вижда, че стойността на работата е

- Работа на реакцията А_R

Тъй като реакцията е перпендикулярна на преместването, тя по дефиниция няма да извършва работа. Все пак това ще бъде проверено :

- Работа на силата на триене А_Т

Силата на триене се определя по формулата Т=mN. Нормалната компонента N може да бъде определена от DАВС на фиг.3 ® N = G sin(60^o)» m g 0.866. Така за силата на триене се получава:

Т = mN = 0.1 m g 0.866 » 0.087 m g.

Посоката на силата на триене е противоположна на посоката на преместването, което значи, че работата ще бъде отрицателна:

А_Т = - Т L = - (0.087mg) (2) = - 0.174 mg

С получените изрази формираме цялата работа, извършена между двата разглеждани момента от движението:

А₁₂ = A_G + А_R + А_Т = mg + 0 - 0.174 mg = 0.836 mg

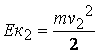Да припомня уравнението, с което ще решим задачата (остана някъде високо горе) ® и другите два члена и 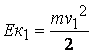. Като ге заместим в израза, ще получим:

.

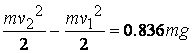Като вземем предвид, че в първия момент скоростта е нула (тялото тръгва от покой), и съкратим масата от двете страни на равенството, ще получим:

и ,

от където:

и окончателно v » 4.05 [m/s].

Изминатият път беше заместен с два метра, а земното ускорение - с 9.81 метра за секунда на квадрат. Поради това резултатът се получи в метри и секунди. На изпита може да бъдете проверен как боравите с мерките и някои величини да Ви бъдат в други дименсии.

ПРОДЪЛЖИ >>>