ДЕФОРМАЦИИ ПРИ ТРИМЕРНО

НАПРЕГНАТО СЪСТОЯНИЕ. ОБОБЩЕН ЗАКОН НА ХУК.

Материалът e разработен по “Д. Панчовски, М. Попова, Приложна механика. ВХТИ, София, 1985”

с помощта на Гергана Иванова (ЕК 282) от кръжока по Техническа механика

При изследване деформациите при тримерно напрегнато състояние приемаме, в съответствие с основните хипотези на приложната механика, че поведението на материала следва закона на Хук и деформациите са малки.

Обобщен закон на Хук

Изразите за относителните надлъжна и напречна деформации при едномерно напрегнато състояние:

и ,

могат да бъдат обобщени за случая на тримерно напрегнато състояние.

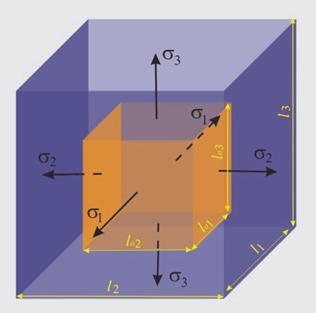
Фиг.1

Да разгледаме елементарен правоъгълен паралелепипед със страни l_o1, l_o2 и l_o3. Паралелепипедът е подложен на външно въздействие, което променя дължината на ръбовете му (l_o1 става l₁ и т.н., фиг.1). Върху стените, на паралелепипеда действат главните напрежения σ₁, σ₂ и σ₃ (положителни). По направление на главните напрежения възникват главните относителни деформации:

ε₁=, ε₂= и ε₃=_.

Стойностите на тези деформации могат да бъдат определени, прилагайки принципа на суперпозицията по следния начин:

В резултат на действието само на напрежението σ₁ относителните надлъжна и напречна деформации на ръбовете на правоъгълния паралелепипед ще бъдат:

а) (1)

Първият индекс показва направлението на относителната деформация, а вторият съвпада с индекса на главното напрежение, което я предизвиква.

Аналогично, вследствие на независимото действие на напреженията σ2 и σ3 се получава:

б) (2)

в) (3)

Главните относителни деформации, предизвикани от едновременното действие на трите главни напрежения ще бъдат съответно равни на:

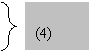ε₁= ε₁₁+ ε₁₂+ ε₁₃

ε₂= ε₂₁+ ε₂₂+ ε₂₃

ε₃= ε₃₁+ ε₃₂+ ε₃₃

При заместване на изразите а), б) и в) уравненията приемат вида:

Тези формули могат да бъдат използвани и в случаите, когато стените на елементарния паралелепипед не съвпадат с главните площадки, тъй като тангенциалните напрежения не предизвикват удължения на ръбовете, а само изменение на правите ъгли между стените. В този случай уравненията (5) приемат вида:

Уравненията (5) и (6) са математически изрази на обобщения закон на Хук. Като приложим в (5) или (6) едно от главните нормални напрежения равно на нула, се получава закона на Хук за двумерно напрегнато състояние.

Обемна деформация

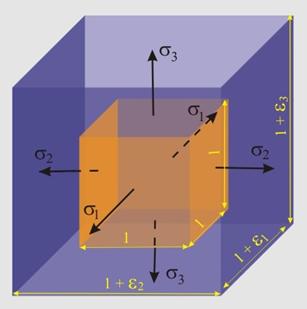
Да разгледаме куб с дължина на ръба 1 (единица), върху стените, на който действат главните нормални напрежения σ₁, σ₂ и σ₃ (положителни) (фиг. 2).

След деформирането дължините на ръбовете на куба стават 1+ε₁, 1+ε₂ и 1+ε_3.

Фиг.2

При известни стойности на главните деформации може да се изчисли относителното изменение на обема ε_V. Първоначалният обем на кула е V₀=1, а след деформирането V=(1+ε₁)(1+ε₂)(1+ε_3.). Относителната обемна деформация се определя по израза:

(7)

Пренебрегвайки безкрайно малките величини от втори () и трети () порядък получаваме:

ε_V =ε₁+ε₂+ε_3. (8)

Замествайки в (8) уравненията (5), изразяващи обобщения закон на Хук, получаваме относителната обемна деформация, изразена чрез главните напрежения:

. (9)

Ако използваме уравнението за средното напрежение в дадена точка

,

получаваме: (10)

Постоянната за даден материал величина се нарича модул на обемната деформация.

От уравнение (10) се вижда, че при μ>0,5, в случаите на всестранен опън (σ₁=σ₂=σ₃=σ>0) обемът на материала трябва да намалява, а при всестранен натиск (σ₁=σ₂=σ₃=σ<0) съответно се увеличава. При реалните материали такъв ефект не се наблядава. Следователно коефициентът на Поасон μ не може да бъде по-голям от 0,5 за всички реални материали.

Специфична потенциална енергия при тримерно напрегнато състояние

При деформираенто на телата в границите на еластичност в тях се натрупва потенциална енергия на деформацията, която е числено равна на извършената работа от външни сили.

За да определим специфичната потенциална енергия при тримерно напрегнато състояние да разгледаме още веднъж куба (фог. 2) стените, на който се главни площадки. В тези площадки действат равномерно разпределени главни напрежения σ₁, σ₂, σ₃. Тъй като площадките имат площ единица, то действащитев тях сили са числено равни на σ₁, σ₂, σ₃, а преместванията им са съответно главните относителни деформации ε₁, ε₂ и ε_3.

Специфичната потенциална енергия, съответстваща на всяко главно напрежение може да се пресметне по формулата , I=1, 2, 3.

Сумарната потенциална енергия на деформирането при тримерно напрегнато състояние отнесена към единица обем е (11)

Замествайки в (11) главните деформации със стойностите им от (5) след някои алгебрични опростявания получаваме:

₍₁₂₎

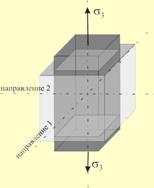
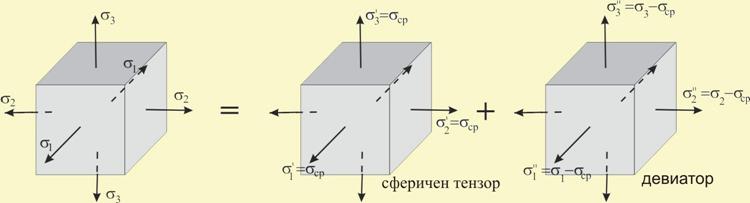
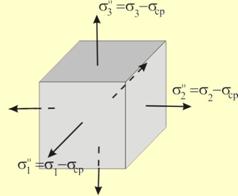
Всяко тримерно напрегнато състояние (σ1, σ2, σ3) условно може да се разглежда като съставено от две напрегнати състояния (фиг.3).

Фиг. 3

Фиг. 4

1. Равномерен всестранен опън/натиск, характеризиращ се от главните напрежения.

(13)

Следователно, съответстващите на главните напрежения главни относителни деформации, при това напрегнато състояние, ще бъдат равни помежду си (ε’₁= ε’₂= ε’₃= ε) и формата на тялото няма да се промени, въпреки изменението на обема му.

Фиг. 5

2. Неравномерното тримерно напрегнато състояние, характеризиращо се с главните напрежения

σ”₁= σ₁- σ_ср; σ”₂= σ₂- σ_ср; σ”₃ =σ₃- σ_ср, (14)

тъй като σ”₁ + σ”₂ + σ”₃ = 0, то според уравнение (9) относителното изменение на обема при това напрегнато състояние ще бъде равно на нула, променя се само формата на тялото.

В съответствие с това и специфичната потенциална енергия може да бъде разгледана като съставна от две компоненти: u=u_V+u_f, където u_V е специфичната потенциална енергия за изменение на обема; u_f – специфичната потенциална енергия за промяна на формата на тялото.

От (13) и (14) следва σ₁= σ`<sub>1</sub>+ σ”<sub>1</sub>; σ<sub>2</sub>= σ`₂ +σ”₂; σ₃ =σ`₃ +σ”₃, откъдето с помощта на (11) намираме

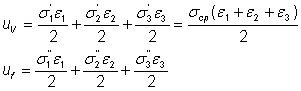(15)

като заместим в (15) главните деформации от (5) и главните напрежения по уравнения (13) и (14) след редица алгебрични преобразования получаваме

(16)